线性数据结构
本章节,我们将介绍最基础、最常用的一类数据结构——线性数据结构。
线性数据结构就像是一排排队的人:
- 每个人(元素)都有明确的前后关系
- 除了第一个和最后一个,每个人都有一个前驱和一个后继
- 数据元素之间是一对一的线性关系
想象一下你正在排队买咖啡,或者整理书架上的书。
这些场景都有一个共同点:元素一个接一个地排列,形成一条线。
在计算机科学中,这种按顺序排列的数据集合,就是线性数据结构。
线性数据结构的特点是:除了第一个和最后一个元素外,每个元素都有且仅有一个 前驱 和一个 后继。
常见线性数据结构:
- 数组:像是一排编号的储物柜,每个柜子有固定位置
- 链表:像是一串手拉手的人,每个人只记住前后的人
- 栈:像是一叠盘子,只能从顶部取放
- 队列:像是排队买票,先来先服务
下图展示了线性数据结构的分类体系,每种结构都有其特定的应用场景和性能特点:
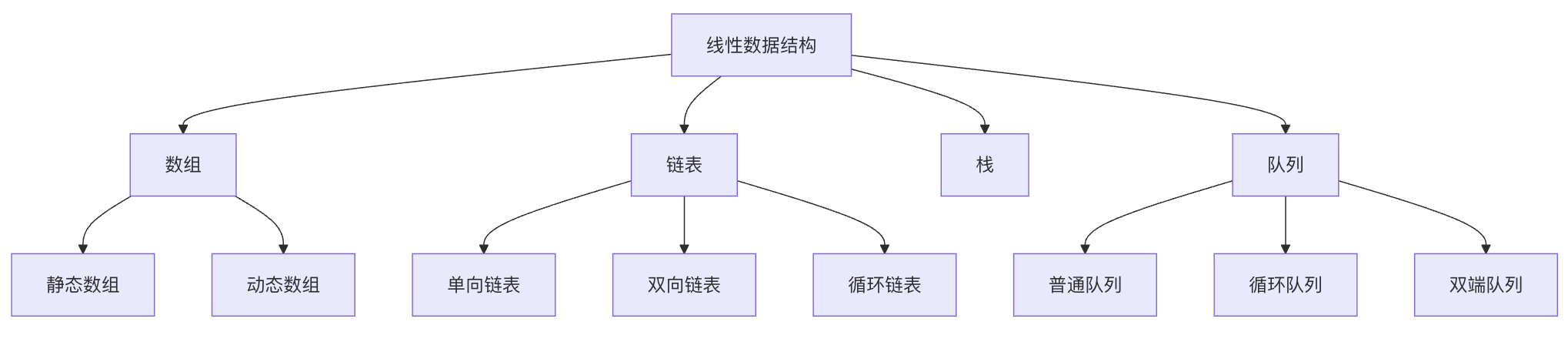
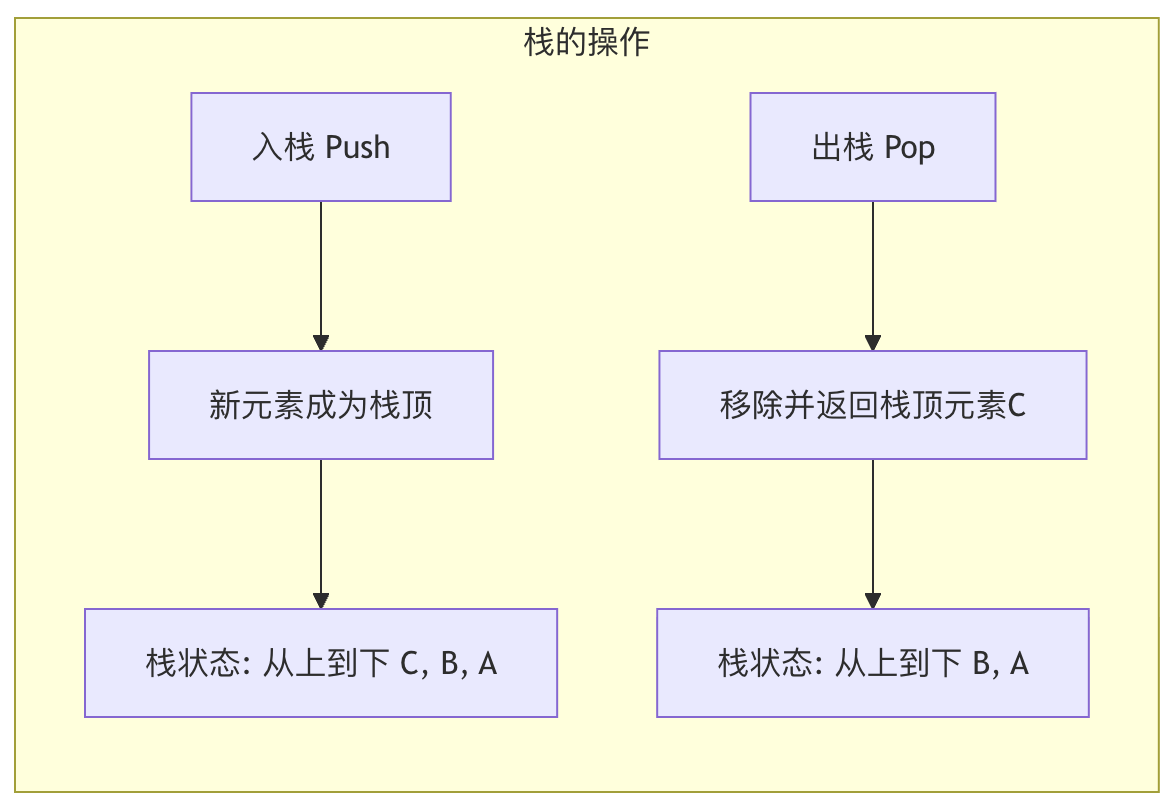
下图展示了栈的基本操作过程,栈遵循LIFO(后进先出)原则:

数组(Array)
静态数组
| 特性 | 描述 | 时间复杂度 |
|---|---|---|
| 访问元素 | 通过索引直接访问 | O(1) |
| 插入元素 | 需要移动后续元素 | O(n) |
| 删除元素 | 需要移动后续元素 | O(n) |
| 空间分配 | 固定大小,预先分配 | O(1) |
动态数组
| 特性 | 描述 | 时间复杂度 |
|---|---|---|
| 访问元素 | 通过索引直接访问 | O(1) |
| 插入元素 | 可能需要扩容和复制 | 平均O(1),最坏O(n) |
| 删除元素 | 需要移动后续元素 | O(n) |
| 空间分配 | 自动扩容 | O(n)(扩容时) |
链表(Linked List)
单向链表
| 操作 | 描述 | 时间复杂度 |
|---|---|---|
| 访问元素 | 需要从头遍历 | O(n) |
| 头部插入 | 直接插入 | O(1) |
| 尾部插入 | 需要遍历到尾部 | O(n) |
| 中间插入 | 需要先找到位置 | O(n) |
| 删除元素 | 需要先找到位置 | O(n) |
双向链表
| 操作 | 描述 | 时间复杂度 |
|---|---|---|
| 访问元素 | 需要从头或尾遍历 | O(n) |
| 头部插入 | 直接插入 | O(1) |
| 尾部插入 | 直接插入(如果有尾指针) | O(1) |
| 中间插入 | 需要先找到位置 | O(n) |
| 删除元素 | 需要先找到位置 | O(n) |
栈(Stack)
| 操作 | 描述 | 时间复杂度 |
|---|---|---|
| push(入栈) | 在栈顶添加元素 | O(1) |
| pop(出栈) | 移除栈顶元素 | O(1) |
| peek(查看) | 查看栈顶元素 | O(1) |
| isEmpty(判空) | 检查栈是否为空 | O(1) |
队列(Queue)
| 操作 | 描述 | 时间复杂度 |
|---|---|---|
| enqueue(入队) | 在队尾添加元素 | O(1) |
| dequeue(出队) | 移除队头元素 | O(1) |
| front(查看队头) | 查看队头元素 | O(1) |
| isEmpty(判空) | 检查队列是否为空 | O(1) |
线性数据结构对比图
数组:数据的固定公寓楼
数组是最简单、最直接的线性数据结构。
我们可以把它想象成一栋 固定楼层数的公寓楼。
基本概念与特点
- 连续存储:数组在内存中占据一块 连续 的空间,就像公寓楼里房间是紧挨着的。
- 固定大小:数组在创建时就需要确定其容量(长度),之后通常不能改变,就像公寓楼盖好后房间数就固定了。
- 索引访问:每个元素(房间)都有一个唯一的编号,称为 索引。在大多数编程语言中,索引从
0开始。你可以通过索引直接、快速地访问任何一个元素,时间复杂度为O(1)。
核心操作与代码示例
让我们用 Python 来演示数组(在 Python 中通常用 list 来模拟,但需注意 Python 的 list 是动态的)的核心操作。
实例
apartment_building = ['101室-张三', '102室-李四', '103室-王五', '104室-空置', '105室-空置']
print("公寓楼住户情况:", apartment_building)
# 2. 访问元素 (通过索引)
# 访问102室
tenant = apartment_building[1] # 索引从0开始,所以1对应第二个元素
print(f"102室的住户是:{tenant}")
# 3. 更新元素
# 104室搬来了新住户赵六
apartment_building[3] = '104室-赵六'
print("赵六入住后:", apartment_building)
# 4. 插入元素 (在末尾添加相对高效,模拟"扩建")
# 假设允许在末尾加盖一间106室
apartment_building.append('106室-孙七')
print("加盖106室后:", apartment_building)
# 5. 删除元素
# 103室的王五搬走了
# 方法一:标记为空置(逻辑删除)
# apartment_building[2] = '103室-空置'
# 方法二:移除该元素,后续元素需要前移(物理删除,效率较低)
removed_tenant = apartment_building.pop(2) # 移除索引为2的元素
print(f"{removed_tenant} 已搬走。")
print("王五搬走后:", apartment_building)
输出:
寓楼住户情况: ['101室-张三', '102室-李四', '103室-王五', '104室-空置', '105室-空置'] 102室的住户是:102室-李四 赵六入住后: ['101室-张三', '102室-李四', '103室-王五', '104室-赵六', '105室-空置'] 加盖106室后: ['101室-张三', '102室-李四', '103室-王五', '104室-赵六', '105室-空置', '106室-孙七'] 103室-王五 已搬走。 王五搬走后: ['101室-张三', '102室-李四', '104室-赵六', '105室-空置', '106室-孙七']
优点与缺点
| 优点 | 缺点 |
|---|---|
| 高速随机访问:通过索引可在常数时间内访问任何元素。 | 大小固定:静态数组一旦创建,容量难以改变。 |
| 内存效率高:连续存储,无需额外空间存储元素间关系。 | 插入/删除成本高:在中间插入或删除元素,需要移动大量后续元素以保持连续性。 |
链表:数据的寻宝火车
当数组的固定大小和插入删除的低效成为问题时,链表就登场了。链表像一列 火车,每节车厢(节点)都装载着货物(数据),并通过挂钩(指针)连接下一节车厢。
基本概念与类型
链表的每个 节点 至少包含两部分:
- 数据域:存储实际的数据值。
- 指针域:存储下一个节点在内存中的地址。
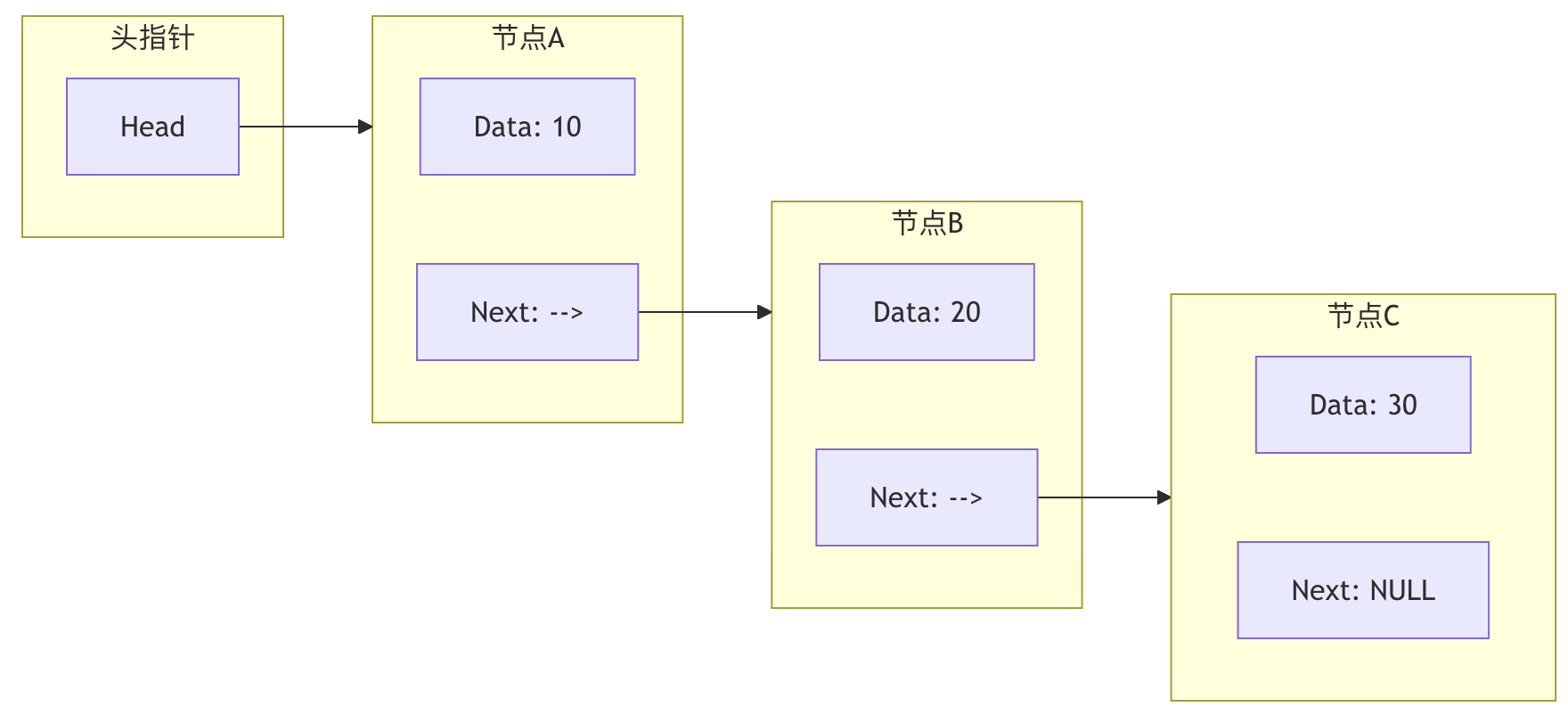
上图展示了一个 单向链表 的结构。头指针指向第一个节点,每个节点的 Next 指针指向下一个节点,最后一个节点的 Next 指向 NULL,表示链表结束。
链表主要类型:
- 单向链表:节点只指向下一个节点。
- 双向链表:节点同时指向前一个和后一个节点,可以双向遍历。
- 循环链表:尾节点指向头节点,形成一个环。
核心操作与代码示例
我们来实现一个简单的单向链表。
实例
"""定义链表节点类"""
def __init__(self, data):
self.data = data # 数据域
self.next = None # 指针域,初始指向空
class LinkedList:
"""定义单向链表类"""
def __init__(self):
self.head = None # 链表头指针
def append(self, data):
"""在链表末尾添加节点"""
new_node = ListNode(data)
if not self.head: # 如果链表为空,新节点成为头节点
self.head = new_node
return
last_node = self.head
while last_node.next: # 遍历到最后一个节点
last_node = last_node.next
last_node.next = new_node # 将新节点挂到末尾
def prepend(self, data):
"""在链表头部添加节点"""
new_node = ListNode(data)
new_node.next = self.head
self.head = new_node
def delete(self, key):
"""删除第一个值为key的节点"""
current_node = self.head
# 如果要删除的是头节点
if current_node and current_node.data == key:
self.head = current_node.next
current_node = None
return
prev_node = None
# 遍历寻找要删除的节点
while current_node and current_node.data != key:
prev_node = current_node
current_node = current_node.next
if current_node is None: # 没找到
return
# 找到后,绕过该节点进行连接
prev_node.next = current_node.next
current_node = None
def print_list(self):
"""打印链表所有元素"""
current_node = self.head
while current_node:
print(current_node.data, end=" -> ")
current_node = current_node.next
print("NULL")
# 测试链表
print("=== 单向链表操作演示 ===")
train = LinkedList()
train.append("车厢1-煤炭")
train.append("车厢2-木材")
train.prepend("车头") # 在头部添加
train.append("车厢3-钢材")
print("初始列车:")
train.print_list() # 输出:车头 -> 车厢1-煤炭 -> 车厢2-木材 -> 车厢3-钢材 -> NULL
train.delete("车厢2-木材")
print("卸下木材后:")
train.print_list() # 输出:车头 -> 车厢1-煤炭 -> 车厢3-钢材 -> NULL
输出:
=== 单向链表操作演示 === 初始列车: 车头 -> 车厢1-煤炭 -> 车厢2-木材 -> 车厢3-钢材 -> NULL 卸下木材后: 车头 -> 车厢1-煤炭 -> 车厢3-钢材 -> NULL
优点与缺点
| 优点 | 缺点 |
|---|---|
| 动态大小:无需预先分配固定空间,可以灵活地增长和缩小。 | 内存开销:每个节点都需要额外空间存储指针。 |
| 高效插入/删除:在已知节点位置时,只需修改指针,无需移动大量元素。 | 顺序访问:无法像数组一样通过索引直接访问,必须从头开始遍历。 |
| 缓存不友好:节点在内存中分散存储,不利于CPU缓存预取。 |
栈:数据的叠盘子
栈是一种 后进先出 的数据结构,就像餐厅里叠放的盘子,你总是取走最上面的那个(最后放上去的)。
基本概念与操作
栈只允许在一端(称为 栈顶)进行插入(入栈)和删除(出栈)操作。另一端称为 栈底。
核心操作:
- push(data):将数据压入栈顶。
- pop():弹出并返回栈顶元素。
- peek() / top():查看栈顶元素但不弹出。
- is_empty():检查栈是否为空。
应用场景与代码示例
栈在计算机科学中应用极广,例如:函数调用栈、浏览器前进后退、表达式求值、括号匹配等。
实例
"""使用列表实现栈"""
def __init__(self):
self.items = []
def push(self, item):
"""入栈"""
self.items.append(item) # 列表末尾作为栈顶
def pop(self):
"""出栈,如果栈空则返回None"""
if not self.is_empty():
return self.items.pop()
return None
def peek(self):
"""查看栈顶元素"""
if not self.is_empty():
return self.items[-1]
return None
def is_empty(self):
"""检查栈是否为空"""
return len(self.items) == 0
def size(self):
"""返回栈的大小"""
return len(self.items)
# 应用示例:括号匹配检查
def is_balanced_parentheses(expression):
"""
检查表达式中的括号是否匹配
例如: (()) 平衡, (() 不平衡
"""
stack = Stack()
# 括号匹配映射
matching_bracket = {')': '(', ']': '[', '}': '{'}
for char in expression:
if char in '([{': # 如果是左括号,入栈
stack.push(char)
elif char in ')]}': # 如果是右括号
if stack.is_empty():
return False # 栈空,说明右括号多了
top_char = stack.pop()
if matching_bracket[char] != top_char: # 检查是否匹配
return False
# 循环结束后,栈应为空
return stack.is_empty()
# 测试栈和括号匹配
print("\n=== 栈与括号匹配演示 ===")
plate_stack = Stack()
plate_stack.push("盘子1")
plate_stack.push("盘子2")
plate_stack.push("盘子3")
print(f"取出最上面的盘子: {plate_stack.pop()}") # 输出:盘子3
print(f"现在最上面的盘子是: {plate_stack.peek()}") # 输出:盘子2
# 测试括号匹配
test_cases = ["((1+2)*3)", "({[ ]})", "((())", ")( )"]
for test in test_cases:
result = "平衡" if is_balanced_parentheses(test) else "不平衡"
print(f"表达式 '{test}' 的括号是 {result} 的。")
输出:
=== 栈与括号匹配演示 ===
取出最上面的盘子: 盘子3
现在最上面的盘子是: 盘子2
表达式 '((1+2)*3)' 的括号是 平衡 的。
表达式 '({[ ]})' 的括号是 平衡 的。
表达式 '((())' 的括号是 不平衡 的。
表达式 ')( )' 的括号是 不平衡 的。
队列:数据的排队通道
队列是一种 先进先出 的数据结构,就像生活中任何需要排队的地方(如超市收银台),先来的人先接受服务。
基本概念与操作
队列允许在一端(称为 队尾)进行插入(入队)操作,在另一端(称为 队头)进行删除(出队)操作。
核心操作:
- enqueue(data):将数据加入队尾。
- dequeue():从队头移除并返回数据。
- front() / peek():查看队头数据但不移除。
- is_empty():检查队列是否为空。
应用场景与代码示例
队列常用于需要按顺序处理任务的场景,如:打印任务队列、消息队列、广度优先搜索等。
实例
class Queue:
"""使用 collections.deque 实现队列"""
def __init__(self):
self.items = deque()
def enqueue(self, item):
"""入队"""
self.items.append(item) # 从右侧(队尾)添加
def dequeue(self):
"""出队,如果队空则返回None"""
if not self.is_empty():
return self.items.popleft() # 从左侧(队头)移除
return None
def front(self):
"""查看队头元素"""
if not self.is_empty():
return self.items[0]
return None
def is_empty(self):
"""检查队列是否为空"""
return len(self.items) == 0
def size(self):
"""返回队列的大小"""
return len(self.items)
# 应用示例:模拟打印任务
print("\n=== 队列与打印任务模拟 ===")
printer_queue = Queue()
# 模拟三个打印任务到达
tasks = ["Alice的简历.pdf", "Bob的报告.doc", "Charlie的图表.png"]
for task in tasks:
printer_queue.enqueue(task)
print(f"任务 '{task}' 已加入打印队列。")
# 处理打印任务
print("\n开始打印...")
while not printer_queue.is_empty():
current_task = printer_queue.dequeue()
print(f"正在打印: {current_task}")
# 模拟打印耗时
print("所有打印任务已完成。")
输出:
=== 队列与打印任务模拟 === 任务 'Alice的简历.pdf' 已加入打印队列。 任务 'Bob的报告.doc' 已加入打印队列。 任务 'Charlie的图表.png' 已加入打印队列。 开始打印... 正在打印: Alice的简历.pdf 正在打印: Bob的报告.doc 正在打印: Charlie的图表.png 所有打印任务已完成。
总结与对比
我们已经学习了四种基础的线性数据结构。下面这个表格帮助你快速回顾和对比它们的核心特性:
| 特性 | 数组 | 链表 | 栈 | 队列 |
|---|---|---|---|---|
| 存储方式 | 连续内存 | 分散内存,通过指针连接 | 基于数组或链表实现 | 基于数组或链表实现 |
| 访问方式 | 随机访问(通过索引) | 顺序访问(必须遍历) | 仅限栈顶(LIFO) | 仅限队头(FIFO) |
| 插入/删除效率 | 尾部快,中间/头部慢(需移动元素) | 已知位置时快(只需改指针) | 栈顶操作,O(1) | 队尾入队,队头出队,O(1) |
| 大小 | 固定(静态数组) | 动态 | 动态 | 动态 |
| 主要应用 | 快速查找、固定集合 | 频繁插入删除、不确定大小 | 函数调用、回溯、括号匹配 | 任务调度、缓冲、BFS |
如何选择?
- 需要 快速随机访问 和已知数据量时,选择 数组。
- 需要 频繁在任意位置插入或删除 元素,且数据量变化大时,选择 链表。
- 需要实现 "撤销" 功能或 反向处理 顺序时,考虑 栈。
- 需要按 "先来后到" 的顺序处理任务时,使用 队列。

点我分享笔记