哈希表

哈希表（Hash Table），也叫散列表，是一种极其高效的数据结构。

哈希表能在平均情况下，以接近 O(1) 的时间复杂度进行数据的插入、删除和查找，这比数组的遍历（O(n)）和二叉搜索树的搜索（O(log n)）要快得多。

操作 数组/链表 哈希表
查找 O(n) O(1)
插入 O(n) O(1)
删除 O(n) O(1)
空间效率 高 中等

哈希表就像是一个智能的储物柜系统：

  • 传统储物柜：你需要记住每个物品放在哪个柜子里（线性查找）
  • 智能储物柜：你告诉管理员物品名称，他直接告诉你柜子编号（哈希查找）

核心思想：
通过哈希函数将键（Key）转换为数组索引，实现快速访问。

生活中的案例：

  • 字典查词：根据单词首字母快速定位到页面
  • 电话簿：按姓氏拼音排序，快速找到联系人
  • 图书馆索书号：根据分类号直接找到书架位置

想象一下，你有一个巨大的图书馆，里面有成千上万本书。

如果你想找一本特定的书，比如《哈利·波特》，你会怎么做？最笨的办法是从第一个书架的第一本书开始，一本一本地找，直到找到为止，这可能需要几个小时甚至几天！

聪明的图书管理员会怎么做呢？他们会使用一个索引系统：根据书名或作者名的某种规则（比如首字母），快速定位到书所在的大致区域，然后只需在那个小区域里寻找即可。这个索引系统的思想，就是哈希表的核心。

基本概念

什么是哈希表？

哈希表是一种通过键（Key）来直接访问值（Value）的数据结构，它利用一个叫做哈希函数的魔法公式，把任意大小的键（比如一个字符串、一个数字或一个对象）转换成一个固定大小的数字，这个数字被称为哈希值或哈希码。然后，用这个哈希值作为数组的索引，将值存储在这个索引对应的数组位置上。

这个过程就像给每个键分配一个唯一的座位号（哈希值），然后告诉它：你的数据就放在这个号码的座位上。当你想找这个数据时，只需要用同样的规则再算一次座位号，就能直接走过去拿到它，而不用一个个座位去问。

核心组件

一个哈希表主要由以下三个核心部分组成：

  1. 键（Key）： 你要存储和查找数据时使用的标识符。比如，在电话簿中，人名就是键。
  2. 值（Value）： 与键相关联的实际数据。在电话簿中，电话号码就是值。
  3. 哈希函数（Hash Function）： 将键映射到数组索引的数学函数。它是哈希表的心脏。

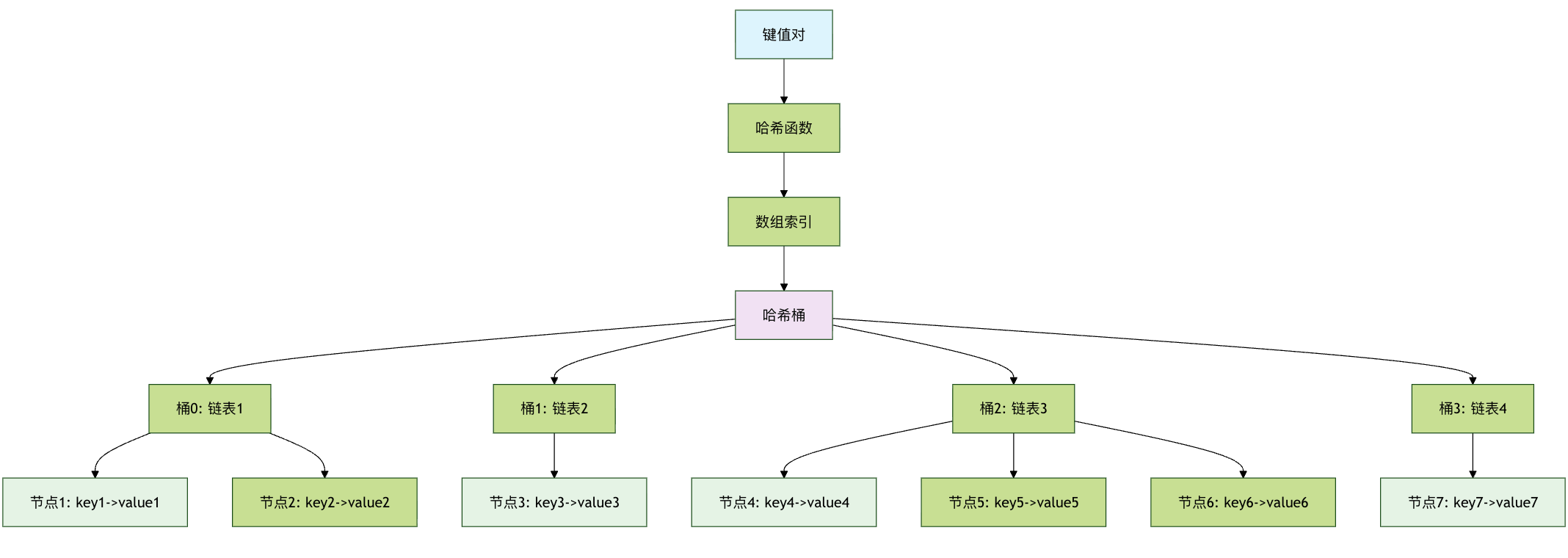
工作原理图解

让我们用一个简单的例子来说明。假设我们要创建一个电话簿，将人名映射到电话号码。

上图清晰地展示了哈希表的工作流程：无论是插入还是查找，都始于一个键，通过哈希函数计算出索引，然后直接对数组的该位置进行操作，从而实现了高速访问。

哈希函数设计

好的哈希函数特性

特性 描述 重要性
确定性 相同输入总是产生相同输出 ⭐⭐⭐⭐⭐
均匀分布 输出均匀分布在哈希表范围内 ⭐⭐⭐⭐⭐
高效计算 计算过程简单快速 ⭐⭐⭐⭐
雪崩效应 输入微小变化导致输出巨大变化 ⭐⭐⭐

常见哈希函数

类型 示例 适用场景
除法取余法 hash = key % table_size 整数键
乘法取整法 hash = floor(key * A % 1 * table_size) 浮点数键
数字分析法 分析数字的分布规律 特定模式数据
平方取中法 hash = (key * key) // 10^(n/2) % table_size 数字键
字符串哈希 逐字符处理 字符串键

冲突解决方法

链地址法（Separate Chaining）

特性 描述 时间复杂度
原理 每个哈希桶维护一个链表
插入 在对应链表头部添加 O(1)
查找 在对应链表中搜索 O(k)，k为链表长度
删除 在对应链表中删除 O(k)
空间开销 需要额外指针存储 较大

开放定址法（Open Addressing）

类型 探测序列 优点 缺点
线性探测 h, h+1, h+2, ... 简单易实现 容易聚集
二次探测 h, h+1², h+2², ... 减少聚集 可能无法探测所有位置
双重哈希 h, h+hash2(key), h+2*hash2(key), ... 分布均匀 计算复杂

哈希表结构图

冲突解决方法对比

深入理解哈希函数

哈希函数是哈希表高效的关键。一个好的哈希函数应该具备以下特点：

  • 确定性： 相同的键必须始终产生相同的哈希值。
  • 高效性： 计算速度要快。
  • 均匀分布： 能将不同的键尽可能均匀地映射到整个数组空间，减少冲突。

一个简单的哈希函数示例

假设我们的键是字符串，数组长度是 10。一个简单的哈希函数可以是将字符串中每个字符的 ASCII 码相加，然后对数组长度取余数。

实例

def simple_hash(key, array_size):
    """
    一个简单的字符串哈希函数。
    :param key: 输入的键（字符串）
    :param array_size: 哈希表数组的大小
    :return: 计算得到的数组索引
    """
    total = 0
    for char in key:
        # 将字符转换为其 ASCII 码值并累加
        total += ord(char)
    # 对数组大小取模，确保索引在数组范围内
    return total % array_size

# 测试我们的哈希函数
keys_to_test = ["Alice", "Bob", "Charlie", "David"]
array_size = 10

print("简单哈希函数测试结果：")
for key in keys_to_test:
    hash_index = simple_hash(key, array_size)
    print(f"  键 '{key}' -> 哈希索引: {hash_index}")

输出结果：

简单哈希函数测试结果：
  键 'Alice' -> 哈希索引: 0
  键 'Bob' -> 哈希索引: 8
  键 'Charlie' -> 哈希索引: 5
  键 'David' -> 哈希索引: 3

这个函数很简单，但它可能不是最好的，因为不同的字符串可能产生相同的和（例如 ab 和 ba），从而导致哈希冲突。

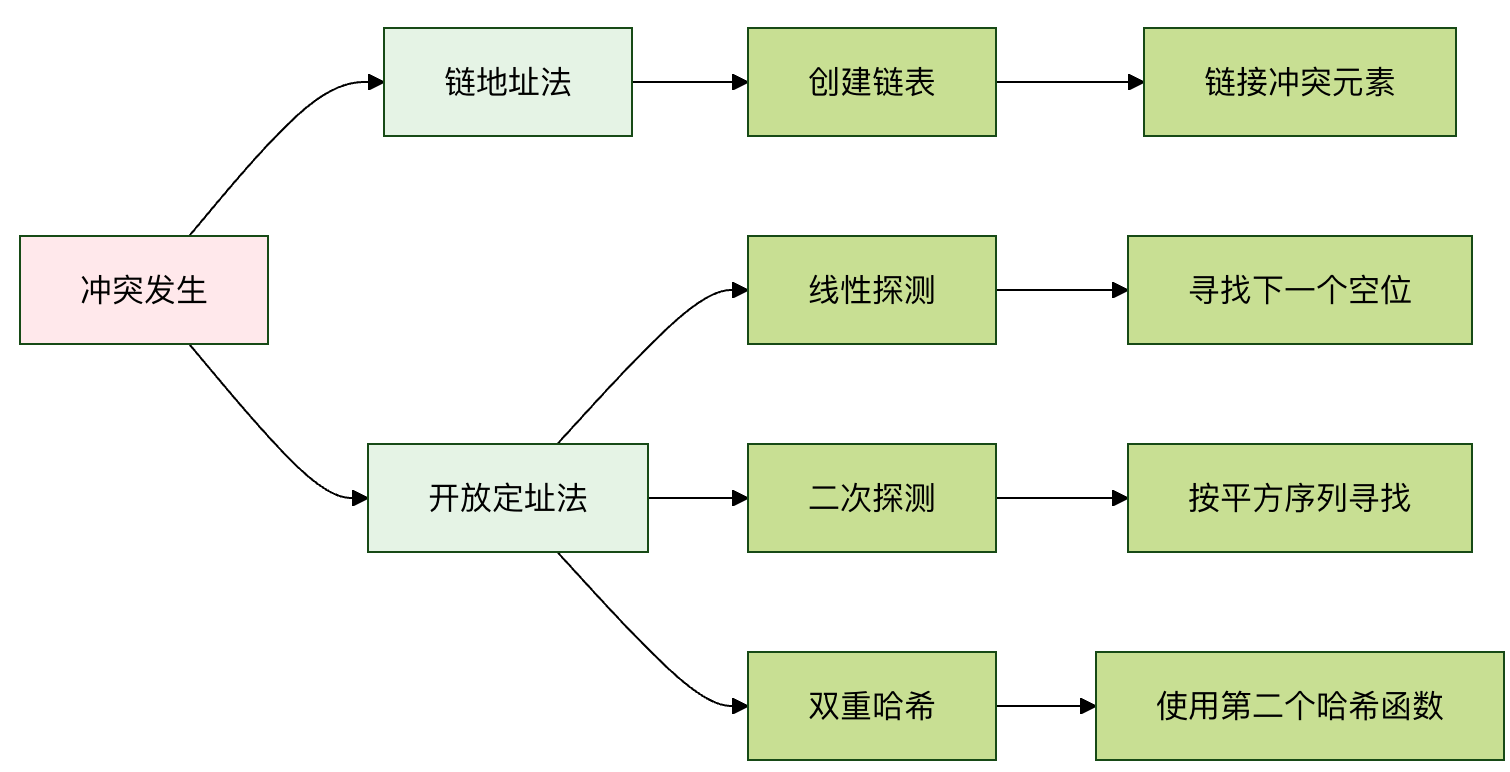
哈希冲突与解决方法

哈希冲突是指两个或更多不同的键，经过哈希函数计算后，得到了相同的数组索引。就像电影院的两个观众被分配了同一个座位号，这显然是个问题。冲突是不可避免的，因为哈希值的范围（数组大小）通常是有限的，而可能的键是无限的。

解决冲突主要有两种经典方法：

方法一：链地址法

这是最常用的方法。它不把数据直接放在数组的每个位置，而是在每个数组位置存放一个链表（或其他数据结构，如红黑树）。当发生冲突时，新的键值对就被添加到这个位置的链表中。

过程描述：

计算键的哈希值，找到数组索引。

  • 如果该索引位置的链表为空，则创建一个新节点存储键值对。

    如果链表不为空（发生冲突），则遍历这个链表。

    • 如果找到了相同的键，则更新其值（或根据需求处理）。
    • 如果没找到相同的键，则将新的键值对添加到链表末尾。

    实例

    class HashTableChaining:
        """使用链地址法解决冲突的哈希表实现。"""

        def __init__(self, size=10):
            """初始化哈希表。
            :param size: 底层数组的初始大小
            """
            self.size = size
            # 创建一个大小为 `size` 的列表，每个元素初始化为一个空列表（代表链表）
            self.table = [[] for _ in range(size)]

        def _hash(self, key):
            """内部哈希函数。这里使用Python内置的hash函数并取模。"""
            return hash(key) % self.size

        def insert(self, key, value):
            """向哈希表中插入一个键值对。"""
            index = self._hash(key)
            bucket = self.table[index] # 获取该索引对应的"桶"（链表）

            # 遍历桶，检查键是否已存在
            for i, (k, v) in enumerate(bucket):
                if k == key:
                    # 键已存在，更新值
                    bucket[i] = (key, value)
                    return
            # 键不存在，添加到链表末尾
            bucket.append((key, value))

        def get(self, key):
            """根据键获取值。如果键不存在则返回None。"""
            index = self._hash(key)
            bucket = self.table[index]

            for k, v in bucket:
                if k == key:
                    return v
            return None # 键不存在

        def delete(self, key):
            """根据键删除键值对。"""
            index = self._hash(key)
            bucket = self.table[index]

            for i, (k, v) in enumerate(bucket):
                if k == key:
                    del bucket[i] # 从链表中删除该节点
                    return True # 删除成功
            return False # 键不存在，删除失败

        def display(self):
            """打印哈希表的所有内容。"""
            for i, bucket in enumerate(self.table):
                print(f"索引 {i}: {bucket}")

    # 使用示例
    print("\n--- 链地址法哈希表示例 ---")
    phone_book = HashTableChaining(5)
    phone_book.insert("Alice", "123-4567")
    phone_book.insert("Bob", "987-6543")
    phone_book.insert("Charlie", "555-1234")
    # 假设"David"的哈希值与"Alice"冲突（为了演示）
    phone_book.insert("David", "111-2222")

    print("插入数据后的哈希表：")
    phone_book.display()

    print(f"\n查找 'Bob' 的电话: {phone_book.get('Bob')}")
    print(f"查找不存在的 'Eve': {phone_book.get('Eve')}")

    phone_book.delete("Charlie")
    print("\n删除 'Charlie' 后的哈希表：")
    phone_book.display()

    输出结果：

    --- 链地址法哈希表示例 ---
插入数据后的哈希表：
索引 0: [('David', '111-2222')]
索引 1: []
索引 2: [('Alice', '123-4567')]
索引 3: [('Charlie', '555-1234')]
索引 4: [('Bob', '987-6543')]

查找 'Bob' 的电话: 987-6543
查找不存在的 'Eve': None

删除 'Charlie' 后的哈希表：
索引 0: [('David', '111-2222')]
索引 1: []
索引 2: [('Alice', '123-4567')]
索引 3: []
索引 4: [('Bob', '987-6543')]

    注意： 为了清晰演示冲突，示例中数组大小设为 5，并使用 hash(key)，实际冲突可能不明显。在 simple_hash 函数下，"Alice" 和 "David" 可能产生相同索引，从而展示链地址法如何在一个索引下存储多个条目。

    方法二：开放地址法

    这种方法将所有元素都存储在数组本身中。当发生冲突时，它会按照某种探测序列（Probing Sequence）在数组中寻找下一个空闲的位置。

    常见的探测方法：

    • 线性探测： 如果位置 i 被占，则尝试 i+1, i+2, i+3... 直到找到空位。
    • 二次探测： 如果位置 i 被占，则尝试 i+1^2, i+2^2, i+3^2...。
    • 双重哈希： 使用第二个哈希函数来计算探测的步长。

    这里我们实现一个简单的线性探测：

    实例

    class HashTableLinearProbing:
        """使用线性探测开放地址法解决冲突的哈希表实现。"""

        def __init__(self, size=10):
            self.size = size
            # 使用一个特殊标记 `None` 表示空位，使用一个标记（如 `'DELETED'`）表示已删除的位置
            # 为了简化，这里只用 `None` 表示空位，查找时遇到 `None` 就停止
            self.keys = [None] * size
            self.values = [None] * size

        def _hash(self, key):
            return hash(key) % self.size

        def insert(self, key, value):
            index = self._hash(key)
            original_index = index

            # 线性探测寻找空位或相同的键
            while self.keys[index] is not None:
                if self.keys[index] == key:
                    # 键已存在，更新值
                    self.values[index] = value
                    return
                index = (index + 1) % self.size # 移动到下一个位置（循环数组）
                if index == original_index:
                    # 已经找了一圈，表满了（实际应用中应该扩容）
                    raise Exception("哈希表已满")

            # 找到空位，插入
            self.keys[index] = key
            self.values[index] = value

        def get(self, key):
            index = self._hash(key)
            original_index = index

            while self.keys[index] is not None:
                if self.keys[index] == key:
                    return self.values[index]
                index = (index + 1) % self.size
                if index == original_index:
                    break # 找了一圈没找到
            return None

        def display(self):
            for i in range(self.size):
                if self.keys[i] is not None:
                    print(f"索引 {i}: 键={self.keys[i]}, 值={self.values[i]}")
                else:
                    print(f"索引 {i}: 空")

    # 使用示例
    print("\n--- 线性探测哈希表示例 ---")
    ht_linear = HashTableLinearProbing(7) # 用小尺寸容易看到探测
    ht_linear.insert("Apple", 10)
    ht_linear.insert("Banana", 20)
    ht_linear.insert("Cherry", 30)
    # 假设"Date"和"Apple"哈希冲突
    ht_linear.insert("Date", 40)

    print("插入数据后的哈希表：")
    ht_linear.display()

    print(f"\n查找 'Banana': {ht_linear.get('Banana')}")
    print(f"查找 'Date' (冲突后插入的): {ht_linear.get('Date')}")

    输出结果：

    --- 线性探测哈希表示例 ---
插入数据后的哈希表：
索引 0: 键=Apple, 值=10
索引 1: 键=Date, 值=40
索引 2: 键=Banana, 值=20
索引 3: 键=Cherry, 值=30
索引 4: 空
索引 5: 空
索引 6: 空

查找 'Banana': 20
查找 'Date' (冲突后插入的): 40

    注意： 在开放地址法中，删除操作比较麻烦，不能简单地将位置置为 None，否则会破坏探测序列。通常使用一个特殊的"已删除"标记。本例为简化未实现删除。

    两种方法的对比

    特性 链地址法 开放地址法
    实现难度 相对简单 相对复杂，尤其是删除操作
    空间开销 需要额外空间存储指针（链表） 所有数据都在数组中，空间利用率可能更高
    冲突影响 冲突只影响同一个桶（链表）的性能 冲突会影响后续插入的位置，可能导致"聚集"现象
    扩容时机 当平均链表长度超过阈值时扩容 当负载因子（元素数/数组大小）超过阈值时扩容
    适用场景 通用，更常见 对缓存友好，适用于已知最大数据量或内存紧张的场景

    哈希表的性能与负载因子

    哈希表的效率高度依赖于一个关键指标：负载因子。

    负载因子 = 哈希表中已存储的元素数量 / 哈希表数组的总大小

    • 负载因子低（如 0.5）： 意味着数组还有很多空位，冲突概率小，操作速度快。
    • 负载因子高（如 0.9）： 意味着数组快满了，冲突概率急剧增加，链表变长或探测距离变长，性能下降。

    为了保持高性能，当负载因子超过某个阈值（例如 0.75）时，哈希表会进行扩容操作：

    1. 创建一个新的、更大的数组（通常是原大小的两倍）。
    2. 遍历旧哈希表中的所有键值对。
    3. 根据新的数组大小，用哈希函数重新计算每个键的索引，并将其插入到新数组中。

    这个过程称为 Rehashing，虽然耗时，但能显著降低负载因子，使哈希表恢复高效。

    实践练习：构建一个单词计数器

    让我们用自制的链地址法哈希表来解决一个实际问题：统计一段文本中每个单词出现的次数。

    我们将使用以下文本作为测试数据（你可以复制到你的代码中）：

    the quick brown fox jumps over the lazy dog the dog is not lazy at all

    实例

    # 练习：使用我们实现的 HashTableChaining 来统计词频
    print("\n=== 实践练习：单词计数器 ===")

    # 1. 创建哈希表实例
    word_counter = HashTableChaining(size=10)

    # 2. 提供的测试文本
    text = "the quick brown fox jumps over the lazy dog the dog is not lazy at all"
    words = text.split() # 将文本分割成单词列表

    print("处理的单词列表:", words)

    # 3. 遍历单词，插入哈希表
    for word in words:
        current_count = word_counter.get(word)
        if current_count is None:
            # 单词第一次出现，计数为1
            word_counter.insert(word, 1)
        else:
            # 单词已存在，计数加1
            word_counter.insert(word, current_count + 1)

    # 4. 输出统计结果
    print("\n单词出现次数统计：")
    # 注意：我们的display方法会按索引打印，这里我们写一个更友好的输出
    all_entries = []
    for bucket in word_counter.table:
        all_entries.extend(bucket) # 将所有桶中的条目合并

    for word, count in all_entries:
        print(f"  '{word}': {count} 次")

    # 5. 验证特定单词
    test_word = "the"
    print(f"\n验证：单词 '{test_word}' 出现了 {word_counter.get(test_word)} 次。")
    test_word = "lazy"
    print(f"验证：单词 '{test_word}' 出现了 {word_counter.get(test_word)} 次。")

    输出结果：

    === 实践练习：单词计数器 ===
处理的单词列表: ['the', 'quick', 'brown', 'fox', 'jumps', 'over', 'the', 'lazy', 'dog', 'the', 'dog', 'is', 'not', 'lazy', 'at', 'all']

单词出现次数统计：
  'the': 3 次
  'quick': 1 次
  'brown': 1 次
  'fox': 1 次
  'jumps': 1 次
  'over': 1 次
  'lazy': 2 次
  'dog': 2 次
  'is': 1 次
  'not': 1 次
  'at': 1 次
  'all': 1 次

验证：单词 'the' 出现了 3 次。
验证：单词 'lazy' 出现了 2 次。

    恭喜！你已经成功使用自己实现的哈希表完成了一个实用的任务。在真实世界的编程中，你几乎不需要自己实现哈希表，因为现代编程语言（如 Python 的 dict、Java 的 HashMap、C++ 的 unordered_map）都提供了高度优化、功能强大的内置哈希表实现。理解其原理，能帮助你更明智、更高效地使用它们。

    总结与要点回顾

    哈希表是什么： 一种通过键直接访问值的高效数据结构，平均时间复杂度为 O(1)。

    核心机制： 哈希函数将键转换为数组索引。

    关键挑战： 哈希冲突——不同的键映射到同一索引。

    解决方案：

    • 链地址法： 每个索引位置存放一个链表来存储冲突的键值对。
    • 开放地址法： 在数组内按照探测序列寻找下一个空位。

    性能关键： 负载因子。负载因子过高时，需要通过扩容和重哈希来恢复性能。

    实际应用： 哈希表是编程的基石，广泛应用于数据库索引、缓存系统、集合成员检查、对象属性存储等无数场景。