双路快速排序
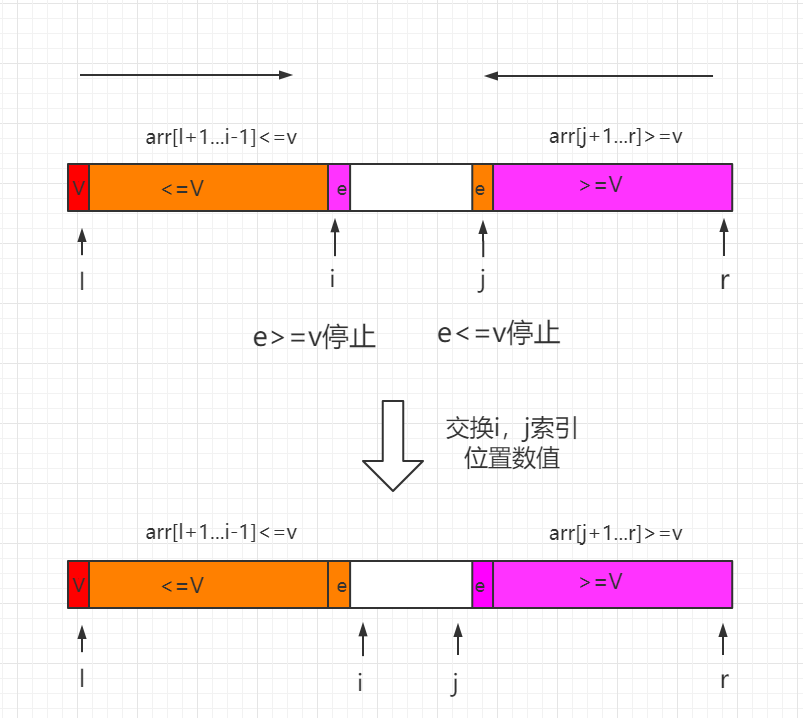
双路快速排序算法是随机化快速排序的改进版本,partition 过程使用两个索引值(i、j)用来遍历数组,将 <v 的元素放在索引i所指向位置的左边,而将 >v 的元素放在索引j所指向位置的右边,v 代表标定值。
适用说明
时间和空间复杂度同随机化快速排序。 对于有大量重复元素的数组,如果使用上一节随机化快速排序效率是非常低的,导致 partition 后大于基点或者小于基点数据的子数组长度会极度不平衡,甚至会退化成 O(n*2) 时间复杂度的算法,对这种情况可以使用双路快速排序算法。
过程图示
使用两个索引值(i、j)用来遍历我们的序列,将 <=v 的元素放在索引 i 所指向位置的左边,而将 >=v 的元素放在索引 j 所指向位置的右边,平衡左右两边子数组。
Java 实例代码
源码包下载:Download
QuickSort2Ways.java 文件代码:
/**
* 双路快速排序
*/
public class QuickSort2Ways {
//核心代码---开始
private static int partition(Comparable[] arr, int l, int r){
// 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
swap( arr, l , (int)(Math.random()*(r-l+1))+l );
Comparable v = arr[l];
// arr[l+1...i) <= v; arr(j...r] >= v
int i = l+1, j = r;
while( true ){
while( i <= r && arr[i].compareTo(v) < 0 )
i ++;
while( j >= l+1 && arr[j].compareTo(v) > 0 )
j --;
if( i > j )
break;
swap( arr, i, j );
i ++;
j --;
}
swap(arr, l, j);
return j;
}
//核心代码---结束
// 递归使用快速排序,对arr[l...r]的范围进行排序
private static void sort(Comparable[] arr, int l, int r){
if (l >= r) {
return;
}
int p = partition(arr, l, r);
sort(arr, l, p-1 );
sort(arr, p+1, r);
}
public static void sort(Comparable[] arr){
int n = arr.length;
sort(arr, 0, n-1);
}
private static void swap(Object[] arr, int i, int j) {
Object t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
// 测试 QuickSort
public static void main(String[] args) {
// 双路快速排序算法也是一个O(nlogn)复杂度的算法
// 可以在1秒之内轻松处理100万数量级的数据
// Quick Sort也是一个O(nlogn)复杂度的算法
// 可以在1秒之内轻松处理100万数量级的数据
int N = 1000000;
Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 100000);
sort(arr);
SortTestHelper.printArray(arr);
}
}
算法原理详解
双路快速排序的核心在于其 双指针分区方法。与单路快排(只从一端扫描)不同,它使用两个指针,分别从待排序子数组的头部和尾部向中间扫描,确保相等的元素不会被全部推向一侧。
核心:双路分区过程
假设我们要对数组 arr 中索引从 left 到 right 的部分进行排序。
选择基准值:从 arr[left...right] 中随机选择一个元素作为基准值 pivot。随机化是为了避免在有序数组上出现最坏情况。
初始化指针:
i = left + 1:从左向右扫描的指针,寻找第一个 大于等于pivot的元素。j = right:从右向左扫描的指针,寻找第一个 小于等于pivot的元素。
扫描与交换循环:
while循环,条件是i <= j。- 内层
while循环:让i不断向右移动,直到arr[i] >= pivot。 - 内层
while循环:让j不断向左移动,直到arr[j] <= pivot。 - 此时,
arr[i]是一个不该在左半部分的"大"元素,arr[j]是一个不该在右半部分的"小"元素。 - 如果此时
i <= j,则交换arr[i]和arr[j],然后i++,j--,继续外层循环。
放置基准值与返回切分点:
- 循环结束后,
i和j已经交错(j < i)。此时arr[left](即基准值)需要被放到正确的位置。 - 将
arr[left]与arr[j]交换。因为j最终停留的位置,其指向的元素是 最后一个小于等于基准值 的元素。 - 返回
j作为新的切分点。此时,arr[left...j-1] <= pivot,arr[j+1...right] >= pivot,且arr[j] == pivot。
递归排序
得到分区点 p 后,对左子数组 arr[left...p-1] 和右子数组 arr[p+1...right] 递归地执行上述过程,直到子数组长度为 1。
代码实现
让我们通过一个完整的 Java 实现来具体理解双路快速排序。
1. 主排序函数
实例
// 公共排序接口
public static void sort(int[] arr) {
if (arr == null || arr.length < 2) {
return; // 边界条件处理:数组为空或只有一个元素,无需排序
}
quickSort(arr, 0, arr.length - 1); // 调用递归的快速排序函数
}
// 递归的快速排序函数
private static void quickSort(int[] arr, int left, int right) {
// 递归终止条件:当左边界大于等于右边界时,子数组已有序或为空
if (left >= right) {
return;
}
// 关键步骤:进行双路分区,并返回分区点的索引
int p = partition(arr, left, right);
// 递归排序左半部分 (left, p-1)
quickSort(arr, left, p - 1);
// 递归排序右半部分 (p+1, right)
quickSort(arr, p + 1, right);
}
}
2. 核心:双路分区函数
这是算法的核心,请结合上面的流程图和注释仔细理解。
实例
private static int partition(int[] arr, int left, int right) {
// 1. 随机选择基准值,并将其交换到 left 位置,避免有序数组下的最坏情况
int randomIndex = left + (int)(Math.random() * (right - left + 1));
swap(arr, left, randomIndex);
int pivot = arr[left]; // 基准值
// 2. 初始化双指针
// i: 从左向右扫描,寻找 >= pivot 的元素
// j: 从右向左扫描,寻找 <= pivot 的元素
int i = left + 1;
int j = right;
// 3. 主循环:当 i 和 j 还未交错时
while (i <= j) {
// 3.1 移动左指针 i:找到第一个 >= pivot 的元素
// 注意边界 i <= right,防止数组越界
while (i <= right && arr[i] < pivot) {
i++;
}
// 3.2 移动右指针 j:找到第一个 <= pivot 的元素
// 注意边界 j >= left+1,因为 left 位置是 pivot 本身
while (j >= left + 1 && arr[j] > pivot) {
j--;
}
// 3.3 检查指针状态
// 如果 i > j,说明扫描已经完成,左右分区已就绪,无需交换
if (i > j) {
break;
}
// 3.4 交换 arr[i] 和 arr[j]
// 此时 arr[i] >= pivot, arr[j] <= pivot,交换它们使得大小元素各归其位
swap(arr, i, j);
// 交换后,移动指针继续扫描
i++;
j--;
}
// 4. 将基准值 pivot 放到最终的正确位置 j 上
// 循环结束后,j 指向最后一个 <= pivot 的元素
swap(arr, left, j);
// 5. 返回分区点的索引 j
return j;
}
// 辅助函数:交换数组中两个元素的位置
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
3. 测试与验证
让我们用一个包含重复元素的数组来测试我们的实现。
实例
public static void main(String[] args) {
// 测试用例1:包含大量重复元素的数组
int[] arr1 = {4, 2, 2, 8, 3, 3, 1, 5, 3, 2};
System.out.println("排序前: " + Arrays.toString(arr1));
TwoWayQuickSort.sort(arr1);
System.out.println("排序后: " + Arrays.toString(arr1));
// 测试用例2:随机生成的大数组
int[] arr2 = new int[20];
Random rand = new Random();
for (int i = 0; i < arr2.length; i++) {
arr2[i] = rand.nextInt(50); // 生成 0-49 的随机数,很可能有重复
}
System.out.println("\n随机数组排序前: " + Arrays.toString(arr2));
TwoWayQuickSort.sort(arr2);
System.out.println("随机数组排序后: " + Arrays.toString(arr2));
// 验证排序结果是否正确
for (int i = 1; i < arr2.length; i++) {
if (arr2[i] < arr2[i-1]) {
System.out.println("排序错误!");
return;
}
}
System.out.println("排序结果验证通过!");
}
}
测试数据输出示例:
排序前: [4, 2, 2, 8, 3, 3, 1, 5, 3, 2] 排序后: [1, 2, 2, 2, 3, 3, 3, 4, 5, 8] 随机数组排序前: [17, 33, 12, 48, 8, 2, 41, ...] 随机数组排序后: [2, 8, 12, 17, 33, 33, 41, 48, ...] 排序结果验证通过!
算法分析与对比
时间复杂度
- 平均情况:$O(n \log n)$。双路快排通过均衡分布重复元素,使得递归树相对平衡。
- 最坏情况:$O(n^2)$。虽然随机化选择基准值大大降低了概率,但当每次分区都极度不平衡时(例如,每次基准值都是当前最小或最大值),仍会出现最坏情况。
- 最好情况:$O(n \log n)$。每次分区都能将数组均匀划分。
空间复杂度
- 主要是递归调用栈所占用的空间。
- 平均深度为 $O(\log n)$,最坏情况下深度为 $O(n)$。
- 因此,平均空间复杂度为 $O(\log n)$,最坏为 $O(n)$。
稳定性
快速排序(包括双路快排)不是稳定的排序算法。因为在分区过程中,非相邻元素的交换会打乱相等元素的原始相对顺序。
单路、双路与三路快排对比
| 特性 | 单路快排 (Lomuto) | 双路快排 | 三路快排 |
|---|---|---|---|
| 分区方式 | 单指针从左向右扫描 | 双指针从两端向中间扫描 | 三指针,将数组分为 <pivot, =pivot, >pivot 三部分 |
| 处理重复元素 | 差,可能导致不平衡分区 | 好,能均衡分布重复元素 | 最优,能一次性处理好所有等于基准值的元素 |
| 代码复杂度 | 简单 | 中等 | 稍复杂 |
| 适用场景 | 教学、无/少重复元素 | 通用,尤其适合可能有重复元素的场景 | 存在大量重复元素的场景 |

点我分享笔记