算法基础与分析方法
在计算机科学的世界里,算法 就是计算机的菜谱,它是一个明确的、有限的、可执行的指令序列,用于解决一个特定的问题或完成一项具体的计算任务。无论是手机上的导航软件为你规划最短路径,还是搜索引擎在毫秒间从海量数据中找出最相关的网页,背后都依赖于精心设计的算法。
理解算法的基础和分析方法,是每一位程序员从代码实现者迈向问题解决者的关键一步。
本文将带你系统地认识算法的核心概念,并学习如何科学地评价一个算法的优劣。
算法的核心特征
一个合格的算法必须具备以下五个基本特征,我们可以用做菜的类比来理解它们:
- 有穷性:算法必须在执行有限步之后结束。就像菜谱不能要求你无限搅拌直到宇宙尽头,它必须给出明确的停止条件。
- 确定性:算法的每一步都必须有确切的定义,没有歧义。例如,加少许盐是不确定的,而加 5 克盐是确定的。
- 可行性:算法中的每一个操作都必须是基本的、可以执行的。你不能在菜谱里写用意念把鸡蛋打散。
- 输入:一个算法有零个或多个输入。这些输入是算法处理的对象,就像菜谱需要的食材。
- 输出:一个算法有一个或多个输出。输出是与输入有特定关系的量,是算法执行的结果,就像最终做好的菜肴。
如何描述算法?
我们可以用多种方式来描述一个算法,最常见的有三种:
1. 自然语言描述
用人类语言(如中文、英文)叙述算法的步骤。优点是易于理解,但缺点是不够精确,容易产生歧义。
示例:找出三个数中的最大值。
- 比较第一个数和第二个数,记住较大的那个。
- 将上一步记住的数与第三个数比较。
- 输出较大的数作为最大值。
2. 流程图
使用图形化的符号表示算法的控制流程。它直观地展示了步骤之间的逻辑关系。
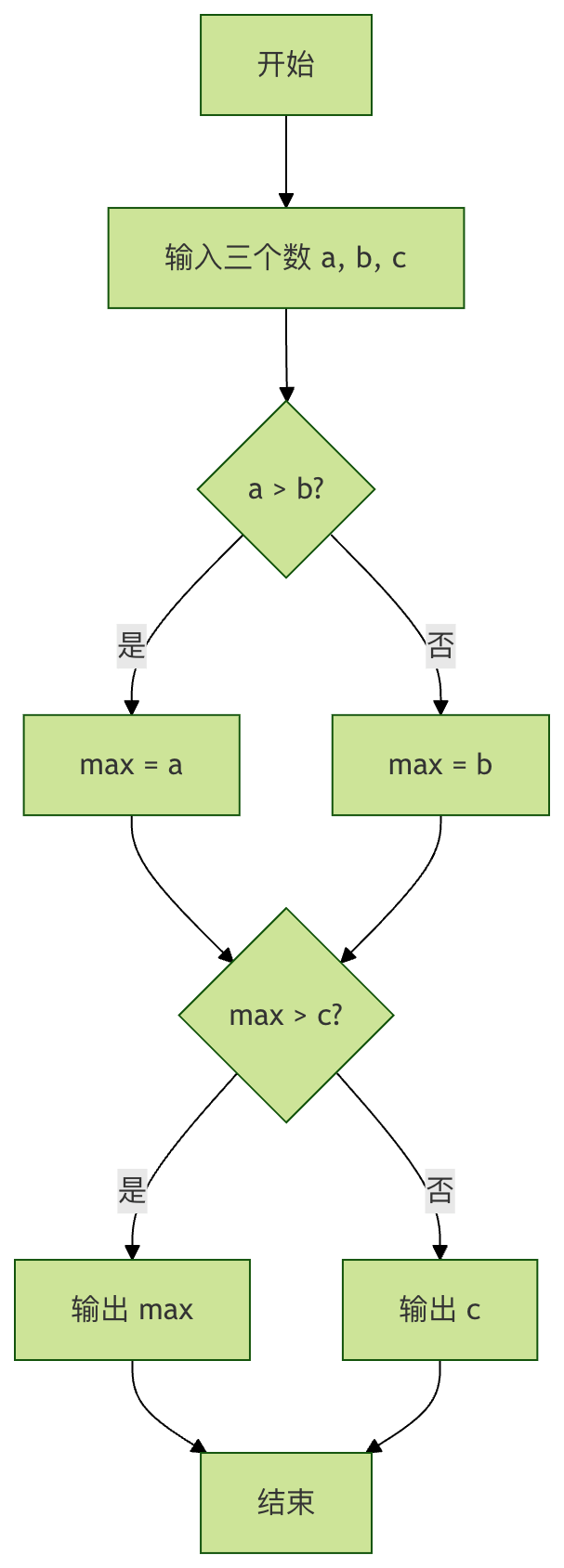
流程图说明:该图清晰地展示了求三数最大值算法的决策过程。菱形代表条件判断,矩形代表处理步骤,箭头指示了程序执行的方向。
3. 伪代码
一种介于自然语言和编程语言之间的描述方式。它使用类似编程语言的结构(如 if, for, while),但忽略具体的语法细节,专注于逻辑表达。
算法:FindMax 输入:三个数字 a, b, c 输出:最大值 max 1. if a > b then 2. max = a 3. else 4. max = b 5. end if 6. if c > max then 7. max = c 8. end if 9. 输出 max
4. 编程语言实现
最终,算法需要被翻译成某种编程语言(如 Python, Java, C++)的代码,才能在计算机上运行。
实例
def find_max(a, b, c):
# 先比较 a 和 b,将较大值赋给 max_value
if a > b:
max_value = a
else:
max_value = b
# 再将 max_value 与 c 比较
if c > max_value:
max_value = c
return max_value
# 测试代码
print(find_max(5, 9, 3)) # 输出:9
print(find_max(-1, 0, 1)) # 输出:1
输出结果:
9 1
算法分析:如何评价算法的好坏?
设计出能解决问题的算法只是第一步,我们还需要判断哪个算法更好。通常我们从两个维度来评估:
1. 时间复杂度
它衡量的是算法运行所需的时间如何随着输入数据规模(n) 的增长而增长。我们关注的不是具体的秒数,而是增长的趋势(称为 渐进时间复杂度)。
常见时间复杂度对比:
| 复杂度 | 名称 | 举例(n=数据量) | 形象比喻 |
|---|---|---|---|
| O(1) | 常数阶 | 数组按索引取值 | "开灯"。无论房间多大,按开关的时间都一样。 |
| O(log n) | 对数阶 | 二分查找 | "翻字典"。每次排除一半,查找速度极快。 |
| O(n) | 线性阶 | 遍历数组 | "数人数"。一个人一个人地数,时间与总人数成正比。 |
| O(n log n) | 线性对数阶 | 快速排序、归并排序 | "先分后治的排序"。比 O(n²) 快很多。 |
| O(n²) | 平方阶 | 简单选择排序、冒泡排序 | "两两握手"。每个人都要和其他所有人握手一次。 |
| O(2ⁿ) | 指数阶 | 求解汉诺塔、暴力穷举 | "细胞分裂"。增长非常恐怖,稍大的 n 就无法承受。 |
如何分析? 关注循环和递归。
- 单层循环:通常是 O(n)。
- 嵌套循环:通常是 O(n²)(如果两层都与 n 相关)。
- 二分策略:通常是 O(log n)。
2. 空间复杂度
它衡量的是算法运行所需的内存空间如何随着输入数据规模(n) 的增长而增长。除了存储输入数据本身,还要考虑算法运行过程中额外申请的数组、变量等。
示例分析:
实例
def find_max_in_list(lst):
max_val = lst[0] # 只用了常数个额外变量
for num in lst:
if num > max_val:
max_val = num
return max_val
# 示例2:空间复杂度 O(n)
def copy_and_double_list(lst):
new_list = [] # 申请了一个与输入列表等长的新列表
for num in lst:
new_list.append(num * 2)
return new_list
实践练习:从排序算法看分析与应用
让我们以经典的 冒泡排序 为例,综合运用以上知识。
算法思想
重复地遍历要排序的列表,一次比较两个相邻元素,如果它们的顺序错误就把它们交换过来。
遍历列表的工作重复进行,直到没有再需要交换的元素,这意味着列表已经排序完成。较小的元素会像气泡一样逐渐浮到数列的顶端。
Python 实现与逐行解析
实例
"""
冒泡排序算法
参数 arr: 待排序的列表
返回值: 排序后的列表(原地修改,也直接返回)
"""
n = len(arr)
# 外层循环:控制总共需要几轮"冒泡"
for i in range(n - 1):
# 假设本轮已经有序,用于优化
swapped = False
# 内层循环:进行一轮冒泡,将最大的元素"沉"到最后
# 每一轮后,最后 i+1 个元素是已排好的,所以范围是 n-1-i
for j in range(0, n - 1 - i):
# 如果前面的元素比后面的大,则交换
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j] # Python 优雅的交换语法
swapped = True # 发生了交换
# 如果本轮一次交换都没发生,说明列表已完全有序,提前结束
if not swapped:
break
return arr
# 测试数据与验证
test_data = [64, 34, 25, 12, 22, 11, 90]
print("排序前:", test_data)
sorted_data = bubble_sort(test_data.copy()) # 使用copy防止原列表被修改
print("排序后:", sorted_data)
# 验证结果是否正确
print("排序是否正确?", sorted_data == sorted(test_data.copy())) # 应与Python内置排序结果一致
输出结果:
排序前: [64, 34, 25, 12, 22, 11, 90] 排序后: [11, 12, 22, 25, 34, 64, 90] 排序是否正确? True
算法分析
- 时间复杂度:
- 最坏与平均情况 O(n²):当列表完全逆序时,需要进行
(n-1) + (n-2) + ... + 1 = n(n-1)/2次比较和交换。 - 最好情况 O(n):当列表已经有序时,加入
swapped标志优化后,只需遍历一次即可发现无交换,提前结束。
- 最坏与平均情况 O(n²):当列表完全逆序时,需要进行
- 空间复杂度 O(1):算法只使用了
i,j,swapped等固定数量的临时变量,是 原地排序 算法。
练习任务
- 手动模拟:用纸笔跟踪算法,对列表
[5, 3, 8, 1]进行排序,写出每一轮冒泡后的列表状态。 - 复杂度实验:修改测试数据,分别用已排序的列表(如
[1,2,3,4,5])和完全逆序的列表(如[5,4,3,2,1])测试,观察循环次数(可以在内层循环加计数器)。 - 尝试改进:你能想出一种与冒泡排序思想类似,但可能效率稍高的排序算法吗?(提示:每次遍历不仅冒一个最大泡,同时冒一个最小泡)。

点我分享笔记