三路排序算法

三路排序算法（Three-Way Partitioning）是一种特殊的快速排序变体，专门为处理包含大量重复元素的数组而优化。它的核心思想是在一次分区过程中，将数组划分为三个部分，而不是传统的两个部分。

三路快速排序是双路快速排序的进一步改进版本，三路排序算法把排序的数据分为三部分，分别为小于 v，等于 v，大于 v，v 为标定值，这样三部分的数据中，等于 v 的数据在下次递归中不再需要排序，小于 v 和大于 v 的数据也不会出现某一个特别多的情况），通过此方式三路快速排序算法的性能更优。

想象一下，你有一大桶混合的彩色弹珠，里面有红色、白色和蓝色三种颜色。你的任务是把它们快速分开，让所有红色弹珠在左边，白色在中间，蓝色在右边，三路排序算法就是解决这类问题的分拣大师。

传统快速排序 vs 三路快速排序

让我们用一个简单的表格来对比两者的区别：

特性 传统快速排序 三路快速排序
分区数量 2个（小于基准、大于基准） 3个（小于基准、等于基准、大于基准）
处理重复元素 效率较低，重复元素可能被多次比较和交换 效率极高，重复元素被集中处理
时间复杂度 平均 O(n log n)，最坏 O(n²) 平均 O(n log n)，最坏 O(n²)
空间复杂度 O(log n)（递归栈） O(log n)（递归栈）
适用场景 通用排序，元素重复率低 元素重复率高，如颜色排序、成绩分段

适用说明

时间和空间复杂度同随机化快速排序。

三路快速排序算法是使用三路划分策略对数组进行划分，对处理大量重复元素的数组非常有效提高快速排序的过程。它添加处理等于划分元素值的逻辑，将所有等于划分元素的值集中在一起。

过程图示

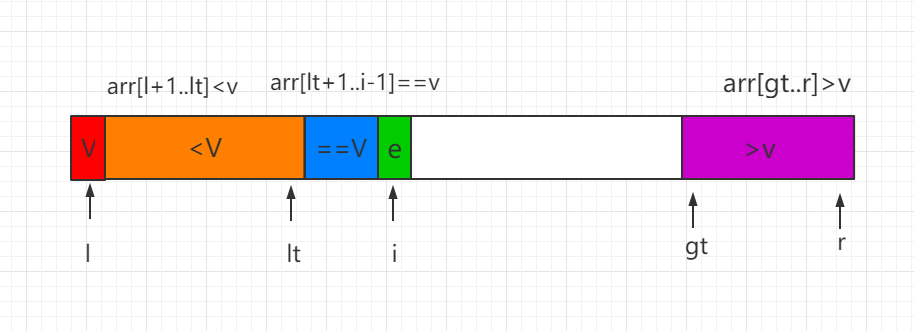
我们分三种情况进行讨论 partiton 过程，i 表示遍历的当前索引位置：

（1）当前处理的元素 e=V，元素 e 直接纳入蓝色区间，同时i向后移一位。

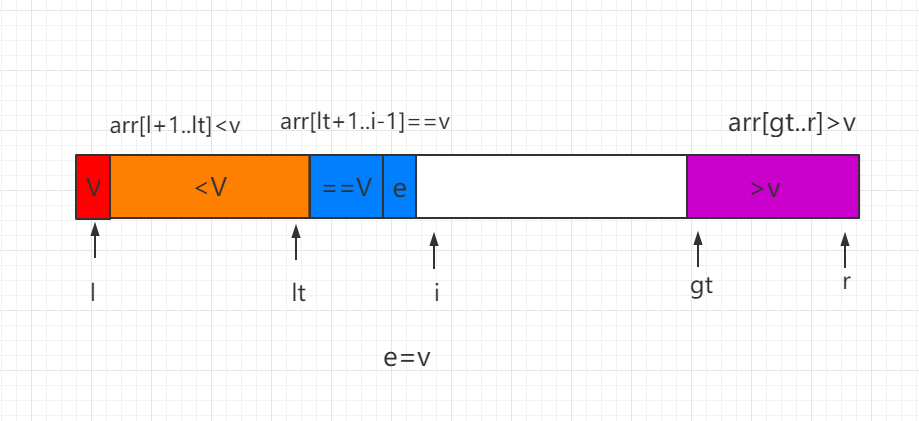
（2）当前处理元素 e<v，e 和等于 V 区间的第一个位置数值进行交换，同时索引 lt 和 i 都向后移动一位

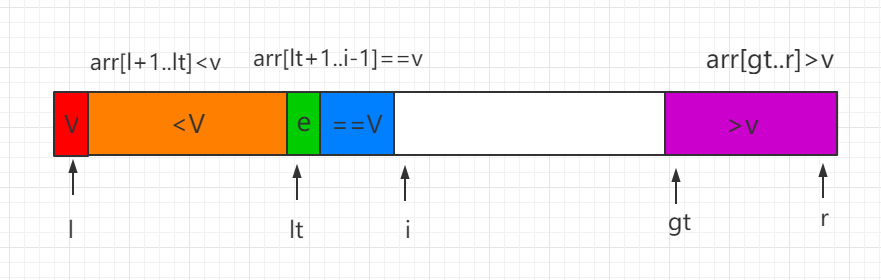
（3）当前处理元素 e>v，e 和 gt-1 索引位置的数值进行交换，同时 gt 索引向前移动一位。

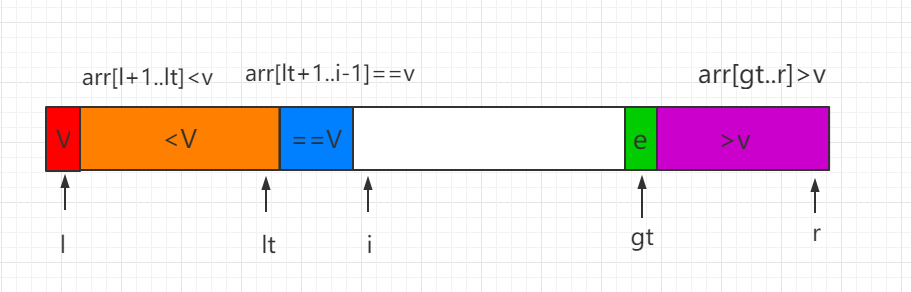
最后当 i=gt 时，结束遍历，同时需要把 v 和索引 lt 指向的数值进行交换，这样这个排序过程就完成了，然后对 <V 和 >V 的数组部分用同样的方法再进行递归排序。

Java 实例代码

源码包下载：Download

QuickSort3Ways.java 文件代码：

package runoob;

/**
 * 三路快速排序
 */
public class QuickSort3Ways {
    //核心代码---开始
    // 递归使用快速排序,对arr[l...r]的范围进行排序
    private static void sort(Comparable[] arr, int l, int r){
        if (l >= r) {
            return;
        }
        // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
        swap( arr, l, (int)(Math.random()*(r-l+1)) + l );
        Comparable v = arr[l];
        int lt = l;     // arr[l+1...lt] < v
        int gt = r + 1; // arr[gt...r] > v
        int i = l+1;    // arr[lt+1...i) == v
        while( i < gt ){
            if( arr[i].compareTo(v) < 0 ){
                swap( arr, i, lt+1);
                i ++;
                lt ++;
            }
            else if( arr[i].compareTo(v) > 0 ){
                swap( arr, i, gt-1);
                gt --;
            }
            else{ // arr[i] == v
                i ++;
            }
        }
        swap( arr, l, lt );
        sort(arr, l, lt-1);
        sort(arr, gt, r);
    }
    //核心代码---结束

    public static void sort(Comparable[] arr){

        int n = arr.length;
        sort(arr, 0, n-1);
    }

    private static void swap(Object[] arr, int i, int j) {
        Object t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }

    // 测试 QuickSort3Ways
    public static void main(String[] args) {

        // 三路快速排序算法也是一个O(nlogn)复杂度的算法
        // 可以在1秒之内轻松处理100万数量级的数据
        int N = 1000000;
        Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 100000);
        sort(arr);
        SortTestHelper.printArray(arr);
    }
}

算法核心思想与工作原理

三路排序算法的精妙之处在于它使用三个指针来追踪数组的不同区域，在一次遍历中完成三项分类。

算法分区状态

让我们通过一个状态图来理解算法的分区过程：

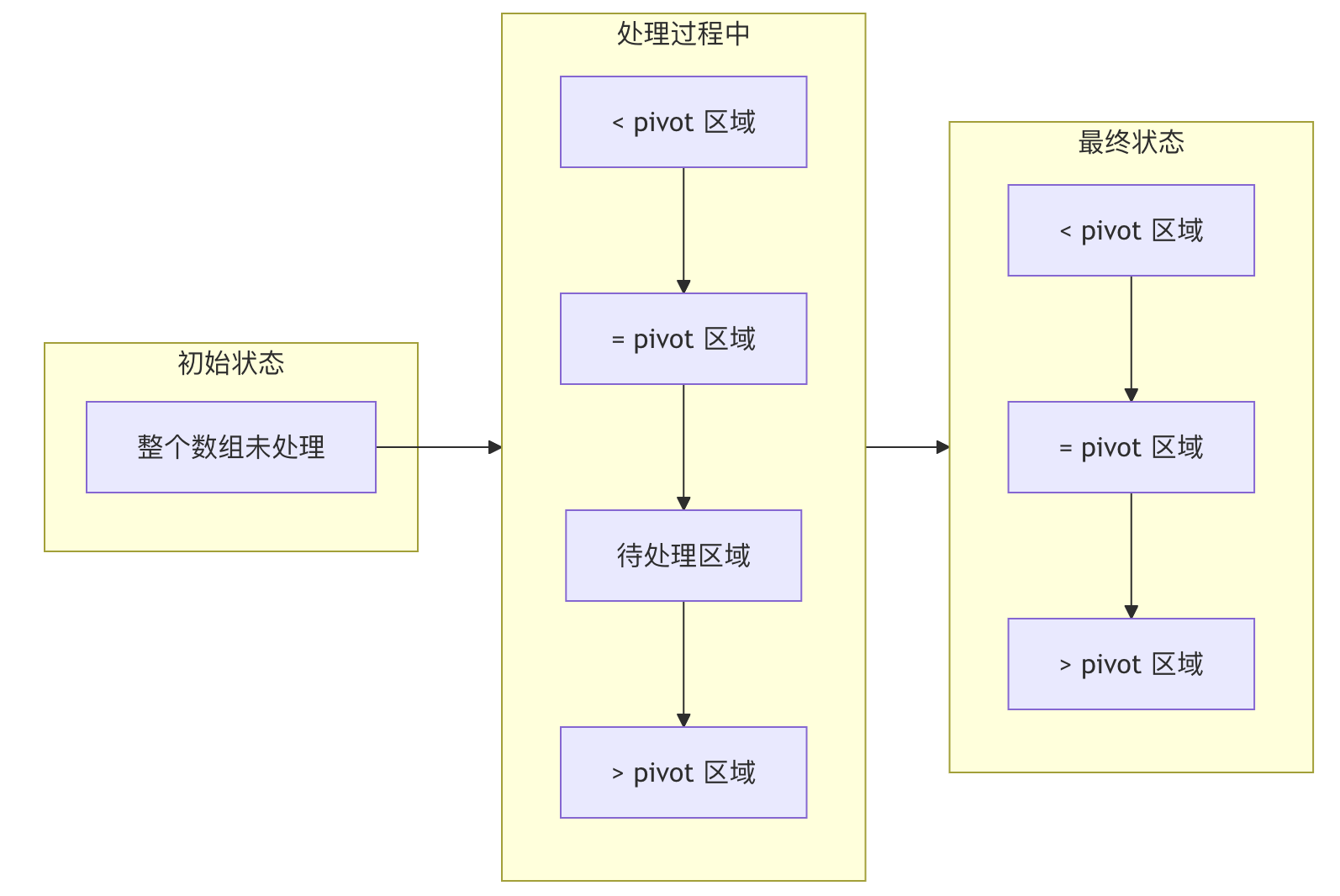
图说明：算法维护三个指针（lt, i, gt）将数组分为四个区域，随着处理进行，待处理区域逐渐缩小，最终形成三个明确的分区。

三个关键指针的作用

  1. lt（less than）指针：指向小于基准值的区域的末尾
  2. i（current）指针：当前正在检查的元素位置
  3. gt（greater than）指针：指向大于基准值的区域的开头

Python 实现

基础三路分区函数

下面是一个标准的三路分区函数的实现，我们将逐行解析：

实例

def three_way_partition(arr, low, high):
    """
    对数组 arr 的 low 到 high 范围进行三路分区
   
    参数:
        arr: 待分区的数组
        low: 分区起始索引
        high: 分区结束索引
       
    返回:
        (lt, gt): 等于基准值区域的左右边界
    """
    # 选择基准值（这里选择第一个元素）
    pivot = arr[low]
   
    # 初始化三个指针
    lt = low      # 小于基准值区域的右边界（初始为low）
    i = low + 1   # 当前检查的元素位置
    gt = high     # 大于基准值区域的左边界（初始为high）
   
    # 主循环：当还有未处理的元素时继续
    while i <= gt:
        if arr[i] < pivot:
            # 情况1：当前元素小于基准值
            # 将其与lt指针的下一个元素交换，扩大小于区域
            arr[lt], arr[i] = arr[i], arr[lt]
            lt += 1
            i += 1
        elif arr[i] > pivot:
            # 情况2：当前元素大于基准值
            # 将其与gt指针的元素交换，扩大大于区域
            arr[i], arr[gt] = arr[gt], arr[i]
            gt -= 1
            # 注意：这里不增加i，因为交换过来的元素还未检查
        else:
            # 情况3：当前元素等于基准值
            # 直接跳过，扩大等于区域
            i += 1
   
    # 返回等于基准值区域的边界
    return lt, gt

完整的三路快速排序实现

基于上面的分区函数，我们可以实现完整的三路快速排序：

实例

def three_way_quicksort(arr, low=0, high=None):
    """
    三路快速排序主函数
   
    参数:
        arr: 待排序的数组
        low: 排序起始索引（默认为0）
        high: 排序结束索引（默认为数组末尾）
    """
    if high is None:
        high = len(arr) - 1
   
    # 递归终止条件：子数组长度小于等于1
    if low >= high:
        return
   
    # 进行三路分区
    lt, gt = three_way_partition(arr, low, high)
   
    # 递归排序小于基准值的部分
    three_way_quicksort(arr, low, lt - 1)
   
    # 递归排序大于基准值的部分
    three_way_quicksort(arr, gt + 1, high)
   
    # 注意：等于基准值的部分已经在正确位置，无需再排序

实战应用示例

示例1：颜色排序问题

这是三路排序算法的经典应用场景，也称为"荷兰国旗问题"。

实例

def sort_colors(colors):
    """
    颜色排序：将只包含0(红), 1(白), 2(蓝)的数组按顺序排列
   
    参数:
        colors: 颜色数组，元素为0, 1, 2
       
    返回:
        排序后的颜色数组
    """
    # 初始化三个指针
    red_ptr = 0          # 红色区域的末尾
    white_ptr = 0        # 当前检查的位置（也是白色区域的末尾）
    blue_ptr = len(colors) - 1  # 蓝色区域的开头
   
    while white_ptr <= blue_ptr:
        if colors[white_ptr] == 0:
            # 红色：交换到红色区域
            colors[red_ptr], colors[white_ptr] = colors[white_ptr], colors[red_ptr]
            red_ptr += 1
            white_ptr += 1
        elif colors[white_ptr] == 1:
            # 白色：留在中间区域
            white_ptr += 1
        else:
            # 蓝色：交换到蓝色区域
            colors[white_ptr], colors[blue_ptr] = colors[blue_ptr], colors[white_ptr]
            blue_ptr -= 1
            # 注意：这里不增加white_ptr，因为交换过来的元素还未检查
   
    return colors

# 测试数据
test_colors = [2, 0, 2, 1, 1, 0, 1, 2, 0, 1, 0, 2]
print("原始颜色数组:", test_colors)
print("排序后颜色数组:", sort_colors(test_colors.copy()))

测试数据说明：上面的数组表示颜色编号（0=红，1=白，2=蓝）。排序后应该是所有0在前，1在中间，2在后。

示例2：学生成绩分段

假设我们需要根据学生成绩进行分段：小于60为不及格，60-80为良好，大于80为优秀。

实例

def categorize_grades(scores):
    """
    将成绩分为三个等级：不及格(<60), 良好(60-80), 优秀(>80)
   
    参数:
        scores: 成绩数组
       
    返回:
        分段后的成绩数组
    """
    if not scores:
        return scores
   
    # 使用三路分区思想，以60和80为界点
    # 先按60分区：不及格 vs 及格以上
    low = 0
    mid = 0
    high = len(scores) - 1
   
    # 第一轮：分离不及格成绩(<60)
    while mid <= high:
        if scores[mid] < 60:
            scores[low], scores[mid] = scores[mid], scores[low]
            low += 1
            mid += 1
        elif scores[mid] <= 80:
            mid += 1
        else:
            scores[mid], scores[high] = scores[high], scores[mid]
            high -= 1
   
    # 第二轮：在及格以上部分中分离良好和优秀
    # 此时low指向第一个良好成绩的位置
    mid = low
    high = len(scores) - 1
   
    while mid <= high:
        if scores[mid] <= 80:
            mid += 1
        else:
            scores[mid], scores[high] = scores[high], scores[mid]
            high -= 1
   
    return scores

# 测试数据
test_scores = [45, 78, 92, 56, 85, 67, 72, 88, 59, 95, 61, 73]
print("原始成绩:", test_scores)
print("分段后成绩:", categorize_grades(test_scores.copy()))
print("说明: 前部分<60, 中间60-80, 后部分>80")

算法复杂度分析

时间复杂度

三路排序算法的时间复杂度分析可以用以下公式表示：

$$ T(n) = O(n) + T(k) + T(n - k - m) $$

其中：

  • $n$ 是数组长度
  • $k$ 是小于基准值的元素数量
  • $m$ 是等于基准值的元素数量
  • $n - k - m$ 是大于基准值的元素数量

最佳情况：每次分区都能将数组均匀分成三部分，时间复杂度为 $O(n \log_3 n)$，实际上仍然是 $O(n \log n)$。

最坏情况：每次分区都极不均匀，时间复杂度为 $O(n^2)$。

平均情况：对于随机数据，平均时间复杂度为 $O(n \log n)$。

空间复杂度

算法使用递归实现，递归深度取决于分区情况：

  • 最佳情况：$O(\log n)$
  • 最坏情况：$O(n)$

可以通过尾递归优化或使用迭代方式减少空间使用。

更多代码展示