神经网络的基本结构
在人工智能的浪潮中,深度学习无疑是其中最耀眼的明星,而构成深度学习核心的,正是神经网络。它模仿人脑神经元的工作方式,通过层层连接与计算,赋予了机器学习和认知的能力。
对于初学者而言,理解神经网络的基本结构,是打开深度学习大门的第一把钥匙。
本文将带你从零开始,一步步拆解神经网络的构成,并用生动的比喻和清晰的代码,让你彻底掌握其工作原理。
神经网络是什么?一个生动的比喻
想象一下,你正在教一个从未见过猫和狗的小朋友区分它们,你会怎么做?
- 你可能会先给他看很多猫和狗的图片。
- 你会指出特征:看,猫的耳朵通常是尖的,脸比较圆;狗的耳朵可能下垂,脸型更长。
- 小朋友的大脑(神经网络)会接收这些图片(输入数据)和你的指导(标签)。
- 他大脑中的神经元会开始工作,尝试找出区分猫和狗的关键模式(如耳朵形状、脸型)。
- 经过多次纠正和学习,他大脑中形成了一个判断模型。下次再看到新动物图片时,他就能自信地说出这是猫或这是狗。
神经网络就是这个小朋友的大脑的简化数学模型, 它是一个由大量人工神经元相互连接构成的网络系统,能够从输入数据中自动学习特征和模式,并用于预测或决策。
神经网络的基本组成单元:神经元
神经元是神经网络最基本的计算单元,它模拟了生物神经元接收信号-处理信号-传递信号的过程。
一个神经元的工作流程
一个典型的人工神经元主要做三件事:
实例
def artificial_neuron(inputs, weights, bias):
"""
模拟一个人工神经元的计算过程。
参数:
inputs: 输入信号列表,例如 [x1, x2, x3]
weights: 对应每个输入的权重列表,例如 [w1, w2, w3]
bias: 偏置项,一个常数
返回:
output: 神经元的输出
"""
# 1. 加权求和:将每个输入乘以其对应的权重,然后加上偏置
weighted_sum = 0
for i in range(len(inputs)):
weighted_sum += inputs[i] * weights[i]
weighted_sum += bias
# 2. 激活函数处理:通过一个非线性函数,决定是否"激活"并输出信号
output = activation_function(weighted_sum)
return output
让我们用一张图和一个表格来更直观地理解:
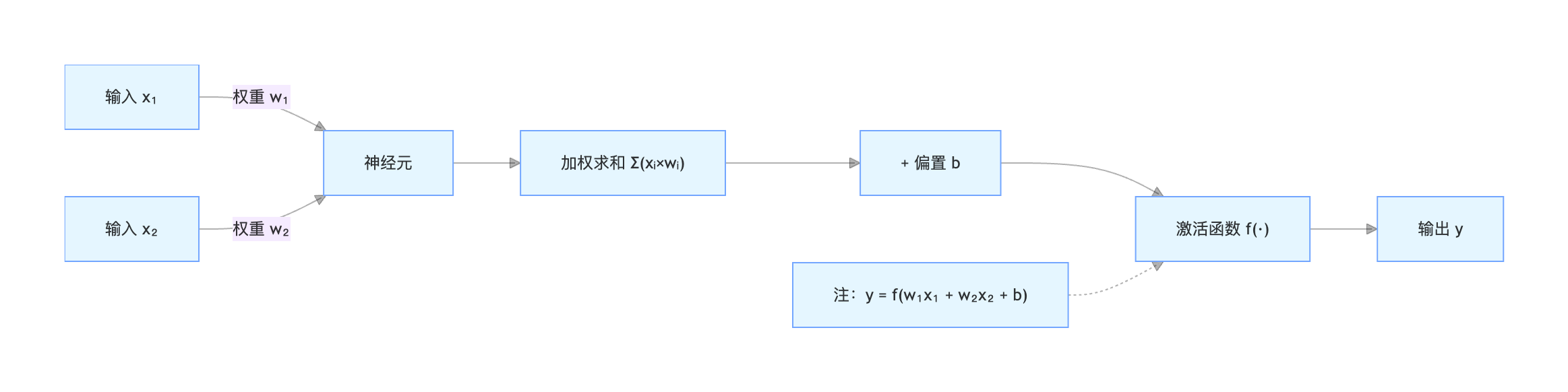
神经元各部件功能详解:
| 部件 | 类比 | 数学表达 | 作用 |
|---|---|---|---|
| 输入 \(x\) | 来自其他神经元的信号 | \( x_1, x_2, ..., x_n \) | 接收外部信息或上一层神经元的输出。 |
| 权重 \(w\) | 信号的重要性 | \(w_1, w_2, ..., w_n\) | 决定每个输入对神经元输出的影响程度。学习的过程就是不断调整这些权重的过程。 |
| 偏置 \(b\) | 神经元的激活阈值 | \(b\) | 一个常数,用于调整神经元激活的难易程度。可以理解为让加权和整体上下移动。 |
| 加权和 \(z\) | 信号总强度 | \(z = (x_1w_1 + x_2w_2 + ... + x_nw_n) + b\) | 对所有输入信号进行综合。 |
| 激活函数 \(f\) | 开关与加工器 | \(a = f(z)\) | 引入非线性。如果没有它,多层网络将退化为单层网络,无法学习复杂模式。 |
常见的激活函数
激活函数为神经网络带来了非线性能力。以下是三个最常用的:
Sigmoid
- 公式:\(f(z) = \frac{1}{1 + e^{-z}}\)
- 特点:将输入压缩到 (0, 1) 之间。常用于二分类问题的输出层。容易导致梯度消失问题。
- 图像:平滑的 S 型曲线。
ReLU (整流线性单元)
- 公式:\(f(z) = max(0, z)\)
- 特点:计算简单,能有效缓解梯度消失问题,是目前最常用的隐藏层激活函数。
- 图像:在原点处转折的折线,负数输出 0,正数原样输出。
Softmax
- 公式:\(f(z_i) = \frac{e^{z_i}}{\sum_{j=1}^{K} e^{z_j}}\)
- 特点:将多个神经元的输出转换为概率分布(所有输出之和为1)。专用于多分类问题的输出层。
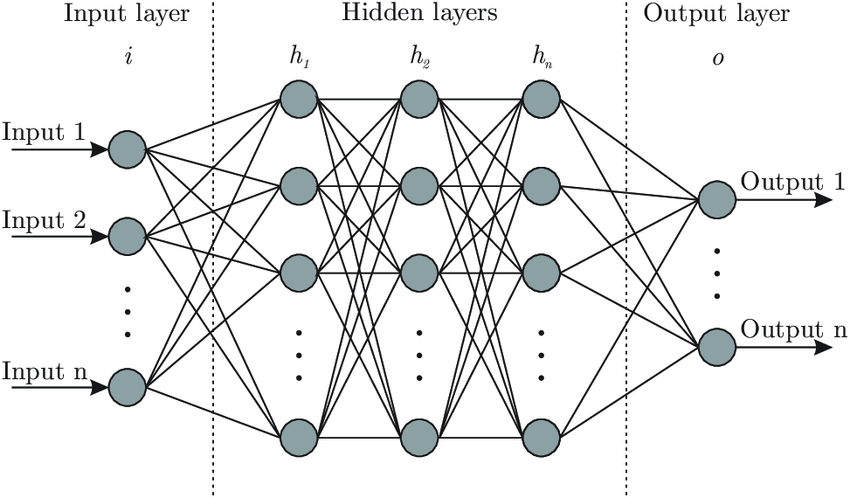
神经网络的层级结构
单个神经元能力有限,就像单个脑细胞无法思考一样。当我们将大量神经元按层组织起来,就形成了强大的神经网络。一个典型的神经网络包含以下三层:
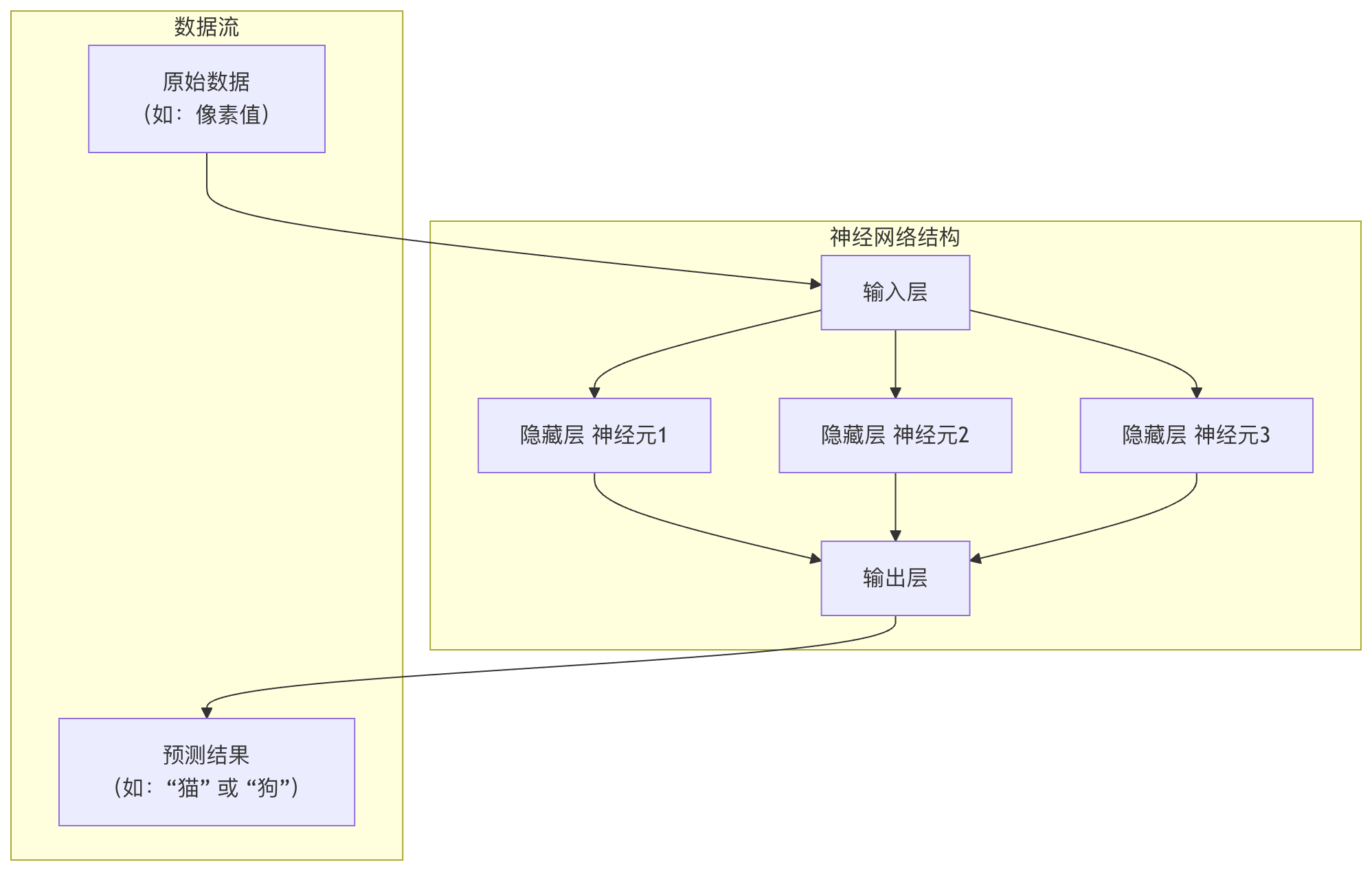
1. 输入层
- 角色:网络的感官,负责接收原始数据。
- 特点:该层的神经元数量通常等于输入数据的特征数。例如,一张28x28像素的灰度图展平后就是784个特征,对应784个输入神经元。输入层不做任何计算,只是传递数据。
2. 隐藏层
角色:网络的大脑,负责进行复杂的特征提取和转换。
特点:
- 介于输入层和输出层之间,可以有一层或多层(深度学习就源于此)。
- 每一层的神经元都接收前一层所有神经元的输出作为输入,并计算自己的输出传递给下一层(这称为全连接)。
- 隐藏层中的神经元使用如 ReLU 等激活函数,引入非线性。
3. 输出层
角色:网络的决策者,输出最终的预测结果。
特点:神经元数量由任务决定。
- 二分类:1个神经元(用Sigmoid)或2个神经元(用Softmax)。
- 多分类(K类):K个神经元(用Softmax)。
- 回归(预测一个连续值):1个神经元(通常不用激活函数)。
实战:用 Python 构建一个神经网络
理论说得再多,不如动手实践。下面我们用 NumPy 库从零开始构建一个最简单的三层神经网络(1个隐藏层),并进行一次前向传播计算。
实例
# 定义激活函数
def sigmoid(x):
"""Sigmoid 激活函数"""
return 1 / (1 + np.exp(-x))
def relu(x):
"""ReLU 激活函数"""
return np.maximum(0, x)
# 初始化一个简单的神经网络
def initialize_network(input_size, hidden_size, output_size):
"""
初始化网络权重和偏置。
参数:
input_size: 输入层神经元数
hidden_size: 隐藏层神经元数
output_size: 输出层神经元数
返回:
network: 包含各层参数的字典
"""
np.random.seed(42) # 设置随机种子,确保每次运行结果一致
network = {}
# 初始化 输入层->隐藏层 的参数
# 权重矩阵形状: (下一层神经元数, 上一层神经元数)
network['W1'] = np.random.randn(hidden_size, input_size) * 0.01
network['b1'] = np.zeros((hidden_size, 1)) # 偏置是列向量
# 初始化 隐藏层->输出层 的参数
network['W2'] = np.random.randn(output_size, hidden_size) * 0.01
network['b2'] = np.zeros((output_size, 1))
return network
# 前向传播函数
def forward_propagation(network, X):
"""
执行前向传播,计算网络输出。
参数:
network: 包含权重和偏置的字典
X: 输入数据,形状为 (特征数, 样本数)
返回:
y_pred: 网络预测输出
cache: 缓存中间结果(用于后续的反向传播)
"""
# 获取参数
W1, b1, W2, b2 = network['W1'], network['b1'], network['W2'], network['b2']
# 第1层计算: 输入层 -> 隐藏层
Z1 = np.dot(W1, X) + b1 # 加权和
A1 = relu(Z1) # 通过ReLU激活函数
# 第2层计算: 隐藏层 -> 输出层
Z2 = np.dot(W2, A1) + b2 # 加权和
A2 = sigmoid(Z2) # 通过Sigmoid激活函数(假设是二分类)
# 缓存中间结果,反向传播时会用到
cache = {'Z1': Z1, 'A1': A1, 'Z2': Z2, 'A2': A2}
return A2, cache
# --- 让我们来运行它!---
# 1. 定义网络结构:2个输入特征,3个隐藏神经元,1个输出(二分类)
input_size = 2
hidden_size = 3
output_size = 1
# 2. 初始化网络
my_network = initialize_network(input_size, hidden_size, output_size)
print("权重 W1 的形状(隐藏层 x 输入层):", my_network['W1'].shape)
print("偏置 b1 的形状:", my_network['b1'].shape)
print("权重 W2 的形状(输出层 x 隐藏层):", my_network['W2'].shape)
# 3. 创建一个样本输入数据(2个特征,1个样本)
# X 的列代表样本,行代表特征
X_sample = np.array([[1.5], [-0.5]]) # 形状 (2, 1)
print("\n输入数据 X:", X_sample.T) # .T 是为了转置打印,便于观看
# 4. 执行前向传播
y_pred, cache = forward_propagation(my_network, X_sample)
print("\n神经网络预测输出 (A2):", y_pred)
# 如果输出 > 0.5,我们可以认为是类别1,否则是类别0
predicted_class = 1 if y_pred > 0.5 else 0
print(f"预测类别: {predicted_class}")
代码解读与输出分析:
初始化:我们创建了一个 2-3-1 结构的网络。W1 是一个 3x2 的矩阵,表示2个输入到3个隐藏神经元的连接权重。
前向传播:
- 输入
[1.5, -0.5]首先与W1相乘并加上b1,得到隐藏层的加权和Z1。 Z1经过 ReLU 函数,得到隐藏层的激活值A1。A1再与W2相乘并加上b2,得到输出层的加权和Z2。Z2最后经过 Sigmoid 函数,压缩到(0,1)之间,作为最终的预测概率A2。
输出:由于权重是随机初始化的,这个未经训练的网络的预测输出 A2 也是一个随机值(接近0.5)。训练神经网络的目的,就是通过大量数据,反复调整 W1, b1, W2, b2,使得 A2 对于不同输入能产生有意义的预测。
核心概念总结与学习路径
通过本文,你已经掌握了神经网络的基石:
| 概念 | 核心要点 |
|---|---|
| 神经元 | 计算单元,完成加权求和 -> 加偏置 -> 激活函数。 |
| 权重与偏置 | 模型需要学习的核心参数,决定了网络的行为。 |
| 激活函数 | 引入非线性(如ReLU, Sigmoid),使网络能学习复杂关系。 |
| 网络层级 | 输入层(接收数据)、隐藏层(特征提取)、输出层(产生预测)。 |
| 前向传播 | 数据从输入层流向输出层,计算预测值的过程。 |
你的学习下一步:
- 损失函数:如何量化网络预测的好坏(如均方误差、交叉熵损失)?
- 反向传播与梯度下降:神经网络如何根据"坏"的程度,自动调整权重和偏置(这是学习的本质)?
- 使用框架实战:用
TensorFlow或PyTorch等现代框架,可以轻松构建和训练更复杂的网络,无需从零开始写NumPy代码。
理解基本结构后,你将发现所有复杂的深度学习模型(如CNN用于图像,RNN用于语音)都是在这个基础结构上,通过改变神经元的连接方式和层级功能演变而来的。现在,你已经拥有了继续探索深度学习广阔世界的地图。
 Linux 命令大全
Linux 命令大全
点我分享笔记