强化学习探索vs开采
在强化学习的世界里,智能体(Agent)就像一个在未知环境中不断学习、成长的探险家。它面临着一个贯穿始终的核心矛盾:是应该探索(Exploration) 未知领域,寻找可能带来更高回报的新路径,还是应该开采(Exploitation) 已知的最佳策略,稳定地获取当前已知的最大收益?这个"探索与开采的权衡"(Exploration-Exploitation Trade-off),是强化学习算法设计中最基本、最关键的挑战之一。理解并处理好这个矛盾,是智能体从新手成长为大师的必经之路。
什么是探索与开采?
让我们先通过一个生活中的比喻来理解这两个核心概念。
想象一下,你每天中午都要选择一家餐馆吃饭。
- 开采(Exploitation):你选择去你已知的、最喜欢的那家餐馆。你知道那里的菜合你口味,价格合适,服务质量稳定。选择开采意味着你基于当前已知的最佳信息做出决策,目的是最大化眼前的确定性收益。在强化学习中,这对应智能体选择当前估值(如Q值)最高的动作。
- 探索(Exploration):你决定尝试一家从未去过的新餐馆。这家新餐馆可能非常难吃,让你后悔不已;但也可能出乎意料地美味,成为你新的最爱。选择探索意味着你为了获取更多关于环境的信息而采取行动,目的是优化长期的未来收益。在强化学习中,这对应智能体随机选择动作,或者选择非当前最优的动作,以更新其对环境模型的认知。
强化学习智能体的目标,不是赢得某一次午餐,而是在无数次午餐选择中,获得最大的长期满足感(累积奖励)。如果只开采不探索,你可能永远发现不了那家更好的新餐馆,长期收益无法达到最优。如果只探索不开采,你可能会浪费大量时间和金钱在糟糕的餐馆上,无法享受已知的最佳选择。
为什么需要权衡?
探索与开采之所以需要权衡,根源在于环境的不确定性和智能体知识的不完整性。
- 信息有限:智能体初始时对环境一无所知,它必须通过探索来收集数据,构建对世界(状态、动作、奖励、转移概率)的认知模型。
- 机会成本:探索未知动作可能会获得较低的即时奖励(甚至惩罚),这相当于为获取信息付出了成本。如果过度探索,会牺牲大量本可获得的短期收益。
- 最优解的动态性:在非平稳环境中,最优策略可能会随时间变化。即使智能体找到了当前最优策略,也需要持续进行一定程度的探索,以适应环境变化,防止策略过时。
因此,一个优秀的强化学习算法必须在"利用现有知识获取收益"和"探索未知以改进知识"之间找到一个动态平衡点。
常见的探索策略
如何将探索机制融入到算法中?以下是几种经典的方法:
ε-贪心策略 (ε-Greedy)
这是最简单、最常用的探索策略。智能体在绝大多数时间(概率为 1-ε)选择当前认为最优的动作(开采),但会以一个小概率 ε(例如 5%)完全随机地选择一个动作(探索)。
实例
def epsilon_greedy(q_values, epsilon=0.1):
"""
实现 ε-贪心策略
Args:
q_values: 一个数组,表示当前状态下每个动作的Q值估计。
epsilon: 探索概率,介于0和1之间。
Returns:
selected_action: 根据策略选出的动作索引。
"""
n_actions = len(q_values)
# 以概率 epsilon 进行探索(随机选择)
if np.random.random() < epsilon:
selected_action = np.random.randint(n_actions)
# 以概率 1-epsilon 进行开采(选择Q值最大的动作)
else:
# 如果多个动作Q值相同,随机选择一个
selected_action = np.random.choice(np.where(q_values == np.max(q_values))[0])
return selected_action
# 示例:假设在某个状态下,三个动作的Q值估计为 [1.5, 2.8, 2.3]
state_q_values = [1.5, 2.8, 2.3]
for i in range(10):
action = epsilon_greedy(state_q_values, epsilon=0.2)
print(f"第{i+1}次选择: 动作 {action} (Q值: {state_q_values[action]:.1f})")
优点:简单易懂,易于实现。 缺点:探索时完全随机,没有利用任何已有信息(比如某个动作虽然非最优,但Q值接近最优,它被探索的概率和Q值很低的糟糕动作是一样的)。
上置信界算法 (Upper Confidence Bound, UCB)
UCB 是一种更"聪明"的探索策略。它的核心思想是:为每个动作的估值加上一个"不确定性奖励"。一个动作被尝试的次数越少,其不确定性就越大,这个奖励项就越高,从而鼓励智能体去尝试它。
动作选择公式通常为: \[ a_t = \arg\max_a \left[ Q(a) + c \sqrt{\frac{\ln t}{N_t(a)}} \right] \]
其中:
Q(a)是动作a当前的平均奖励估计(开采项)。N_t(a)是到时刻t为止动作a被选择的次数。c是一个平衡参数,控制探索的强度。ln t是总时间步的对数。- 根号项就是"不确定性奖励"或"探索奖励"。动作被选得越少(
N_t(a)小),这项的值就越大。
实例
import math
class UCB:
def __init__(self, n_actions, c=2):
self.n_actions = n_actions
self.c = c # 探索参数
self.Q = np.zeros(n_actions) # 动作价值估计
self.N = np.zeros(n_actions) # 动作选择次数
self.total_steps = 0
def select_action(self):
self.total_steps += 1
# 确保每个动作至少被选择一次
if np.any(self.N == 0):
action = np.random.choice(np.where(self.N == 0)[0])
else:
# 计算每个动作的UCB值: Q(a) + c * sqrt(ln(t) / N(a))
ucb_values = self.Q + self.c * np.sqrt(np.log(self.total_steps) / self.N)
action = np.argmax(ucb_values)
return action
def update(self, action, reward):
"""更新动作的价值估计"""
self.N[action] += 1
# 增量更新Q值: NewEstimate = OldEstimate + (1/N) * (Target - OldEstimate)
self.Q[action] += (reward - self.Q[action]) / self.N[action]
# 模拟一个多臂老虎机问题,每个臂的真实奖励概率不同
true_means = [0.1, 0.5, 0.9] # 三个臂的真实平均奖励
n_actions = len(true_means)
bandit = UCB(n_actions, c=2)
total_reward = 0
for step in range(1000):
action = bandit.select_action()
# 模拟拉动老虎机臂,以一定概率获得奖励1,否则为0
reward = 1 if np.random.random() < true_means[action] else 0
bandit.update(action, reward)
total_reward += reward
print(f"UCB策略在1000步后获得的总奖励: {total_reward}")
print(f"各动作被选择的次数: {bandit.N}")
print(f"各动作的Q值估计: {bandit.Q}")
优点:探索更有目的性,会优先探索不确定性高(尝试次数少)的动作,能更快地收敛到最优动作。 缺点:需要维护每个动作被选择的次数,在动作空间连续或巨大时可能不适用。
汤普森采样 (Thompson Sampling)
这是一种基于贝叶斯思想的概率性方法。智能体为每个动作的奖励分布(例如伯努利分布的参数 θ_a)维护一个先验分布(如 Beta 分布)。每一步,智能体从每个动作的后验分布中采样一个可能的奖励参数 θ_a,然后选择采样值最大的那个动作执行。收到真实奖励后,再根据结果更新该动作的后验分布。
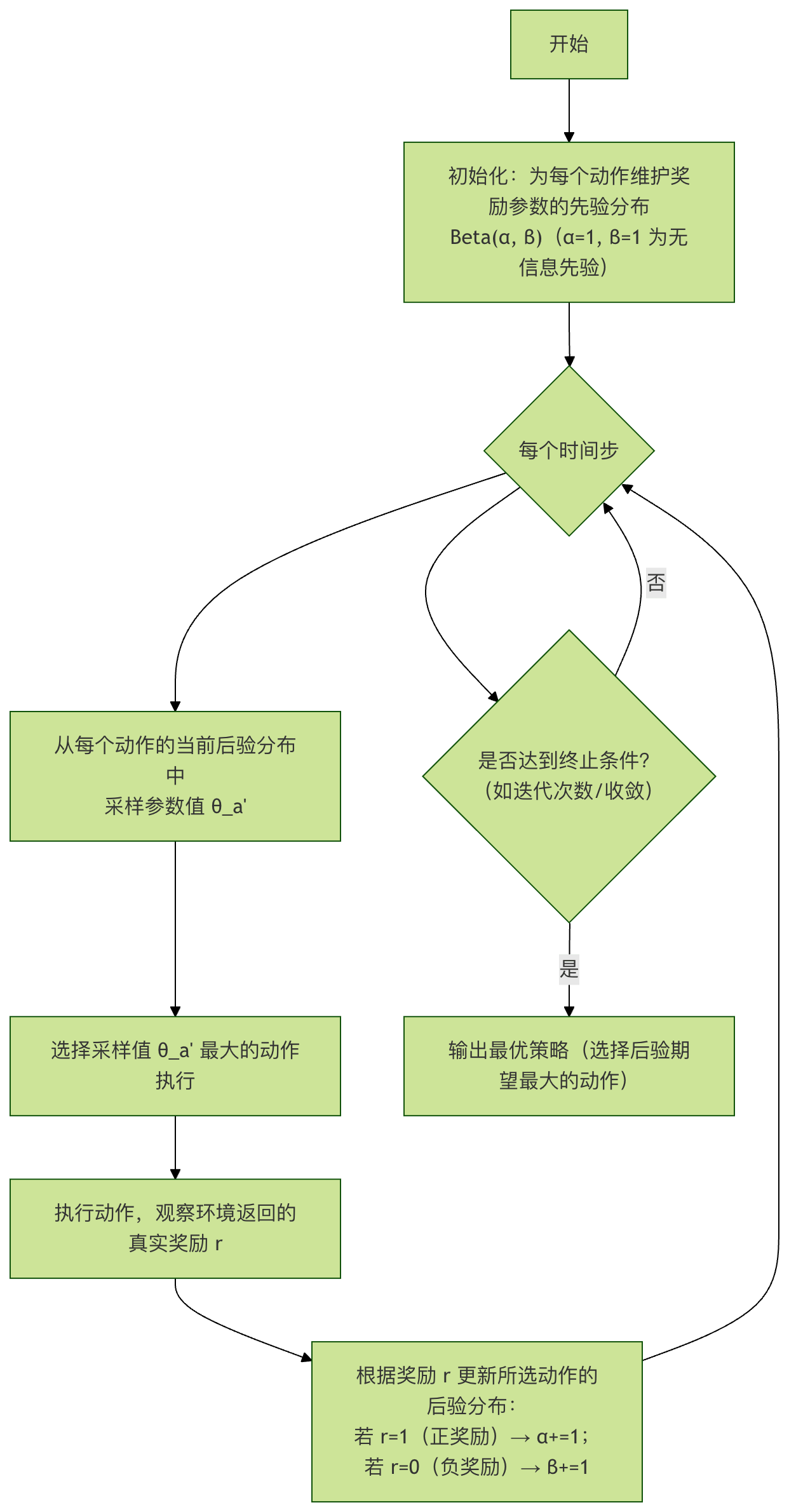
过程说明:
- 初始化:为每个动作
a假设其获得奖励的概率θ_a服从 Beta(α=1, β=1) 分布,这是一个均匀先验。 - 采样:每一步,从每个动作
a的当前 Beta(α_a, β_a) 分布中独立采样一个值θ_a'。 - 选择:执行采样值
θ_a'最大的动作。 - 更新:如果获得奖励
r=1,则将该动作的α加1;如果r=0,则将β加1。这相当于用观测数据更新了贝叶斯后验分布。
优点:自然地平衡探索与开采,理论性质优良,在实践中往往表现非常出色。 缺点:需要假设奖励分布的形式,并且计算可能比 ε-贪心更复杂。
探索与开采的动态平衡
在实际应用中,探索策略往往不是静态的,而是随着智能体的学习进程动态调整的。
- 初期重探索:在训练刚开始时,智能体对环境一无所知,应该设置较高的探索率(如较大的
ε或c),广泛收集数据。 - 后期重开采:随着学习的进行,智能体对环境的认知越来越准确,应该逐渐降低探索率(例如让
ε随时间衰减),将重心转移到利用已学到的优秀策略上,以稳定获得高回报。
这种动态调整的过程,模拟了人类"从广泛尝试到精益求精"的学习过程。
实践练习:对比不同策略
让我们设计一个简单的实验,在经典的"多臂老虎机"问题上对比 ε-贪心 和 UCB 策略的性能。
任务:
- 创建一个有 5 个臂的老虎机,每个臂的真实奖励概率分别为
[0.1, 0.2, 0.8, 0.5, 0.3]。 - 分别实现 ε-贪心(ε=0.1)和 UCB(c=2)策略。
- 让每个策略运行 2000 步,记录每一步的即时奖励和累积奖励。
- 绘制累积奖励随时间步变化的曲线,并观察哪个策略能更快、更稳定地获得更高的总奖励。
思考:
- 尝试调整 ε 和 c 参数,观察对结果有什么影响?
- 如果最优臂(概率0.8)和次优臂(概率0.5)的差距变小,策略的表现会如何变化?
- 在更复杂的强化学习环境(如
Gym中的游戏)中,如何将这些探索策略与 Q-Learning、DQN 等算法结合?

点我分享笔记