概率思维
想象一下,你正在教一个朋友识别猫和狗的照片,你不会说:这张图100%是猫,而可能会说:这张图看起来有 90% 的可能是猫,因为它有尖耳朵和胡须。这种可能性的表述,正是概率思维的核心。
在现实世界中,机器学习模型处理的数据几乎总是充满不确定性的:图像可能模糊、语音可能有噪音、用户行为难以预测。概率为我们提供了一套严谨的数学语言,来描述、量化和处理这种不确定性。它不仅是高级模型(如贝叶斯网络、高斯过程)的基础,更是理解模型输出、评估预测信心和做出稳健决策的关键。
简而言之,概率思维是将猜测转化为可量化的信心的桥梁,是机器学习从硬编码规则迈向智能推理的重要一步。
核心概率概念快速入门
在深入机器学习应用之前,我们需要建立几个基础的概率概念。
1. 概率是什么?
概率是对某个事件发生的可能性的度量,范围在 0 到 1 之间。
P(A) = 0:事件 A 不可能发生。P(A) = 1:事件 A 必然发生。0 < P(A) < 1:事件 A 以一定的可能性发生。
在机器学习中,一个事件可以是:这张图片是猫、用户明天会点击这个广告、下一个单词是你好。
2. 条件概率:世界是相互关联的
条件概率 P(A|B) 表示在事件 B 已经发生的条件下,事件 A 发生的概率。这是机器学习中至关重要的概念。
生活化比喻:
P(下雨):今天下雨的一般概率(先验概率)。P(下雨 | 乌云密布):在已经看到"乌云密布"的条件下,今天下雨的概率(后验概率)。显然,后者的概率值会更高。
公式:
P(A|B) = P(A 且 B) / P(B),要求 P(B) > 0。
3. 贝叶斯定理:从结果反推原因
贝叶斯定理是条件概率的一个华丽应用,它教会我们如何用新证据(数据)来更新我们对一个假设的信念。
公式:
P(假设 | 数据) = [ P(数据 | 假设) * P(假设) ] / P(数据)
让我们拆解这个"魔法公式":
P(假设):先验概率。在看到任何数据之前,我们对假设的初始信念。- 例如:在收到邮件前,我们认为任何邮件是垃圾邮件的概率是 30%。
P(数据 | 假设):似然度。如果假设成立,我们观察到当前这批数据的可能性有多大。- 例如:如果一封邮件确实是垃圾邮件,那么它里面出现"免费"、"获奖"这些词的概率有多高。
P(数据):证据。观察到当前数据的总体概率,通常是一个归一化常数。P(假设 | 数据):后验概率。在观察到数据之后,我们对假设更新后的信念。这是我们最终追求的目标!- 例如:在看到了邮件中包含"免费"、"获奖"这些词后,这封邮件是垃圾邮件的更新概率是 95%。
贝叶斯定理的精髓:它提供了一个系统性的框架,将我们的先验知识(P(假设))与观测到的数据(P(数据|假设))结合起来,得到更准确的更新后认知(P(假设|数据))。
第二部分:概率在机器学习中的三大角色
概率思维渗透在机器学习的各个环节,主要扮演以下三种角色:
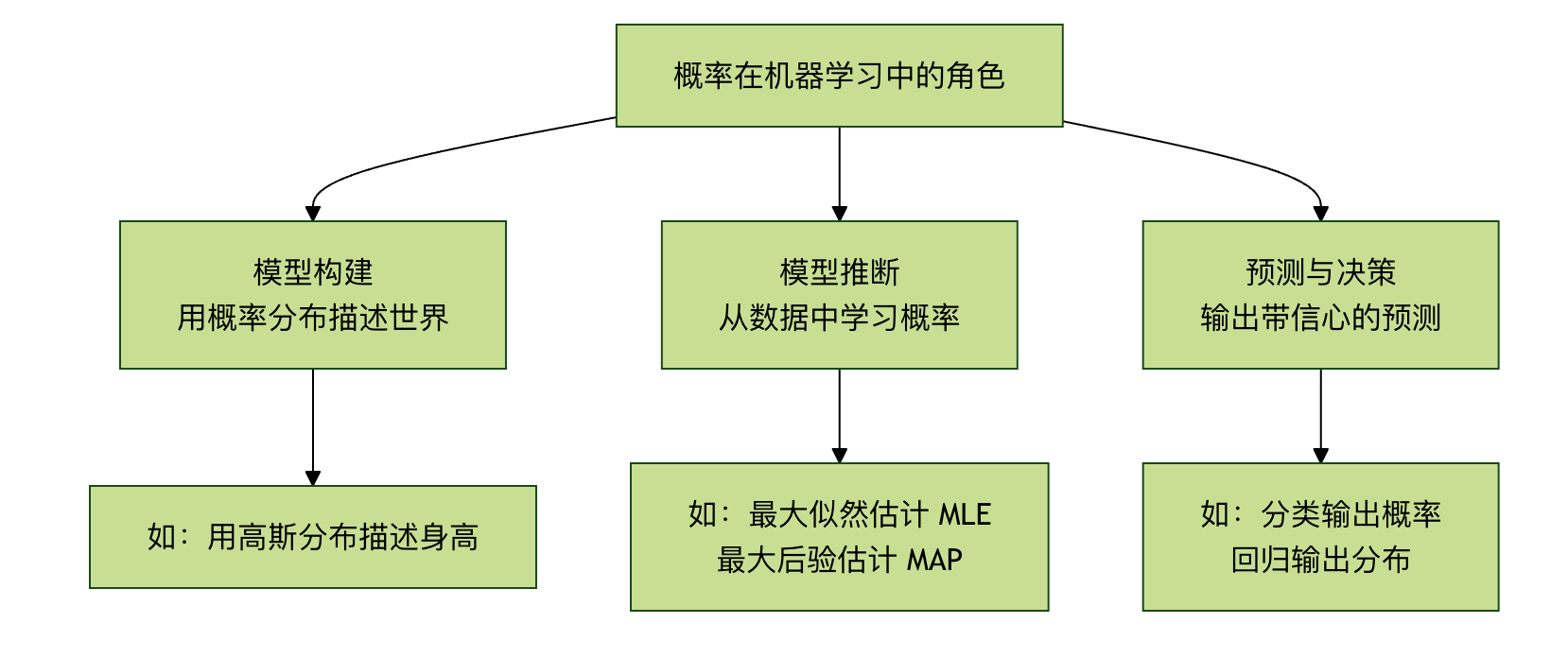
角色一:模型构建 —— 用概率描述世界
许多机器学习模型本质上是一个概率模型。我们假设观测到的数据是由某个潜在的概率分布生成的。
示例 1:逻辑回归
它直接输出一个概率值。对于一个二分类问题(猫/狗),逻辑回归模型不会只说"这是猫",而是输出 P(类别=猫 | 图像数据)=0.9,表示模型有 90% 的信心认为这是猫。
示例 2:朴素贝叶斯分类器
直接应用贝叶斯定理进行分类。它假设特征之间相互独立,计算 P(垃圾邮件 | 词1, 词2...),并选择概率更高的类别。
实例
# 假设我们已从数据中统计出以下概率(似然和先验)
P_单词_给定_垃圾 = {"免费": 0.8, "会议": 0.1} # 在垃圾邮件中,"免费"出现的概率
P_单词_给定_正常 = {"免费": 0.1, "会议": 0.9} # 在正常邮件中,"会议"出现的概率
P_垃圾 = 0.3 # 先验概率:任意邮件是垃圾邮件的概率
P_正常 = 0.7 # 先验概率:任意邮件是正常的概率
# 对于一封包含"免费"和"会议"的邮件,计算它是垃圾邮件的后验概率(简化计算)
# 根据贝叶斯公式(忽略证据分母,因为比较时抵消)
score_垃圾 = P_单词_给定_垃圾["免费"] * P_单词_给定_垃圾["会议"] * P_垃圾
score_正常 = P_单词_给定_正常["免费"] * P_单词_给定_正常["会议"] * P_正常
print(f"属于垃圾邮件的得分: {score_垃圾:.4f}")
print(f"属于正常邮件的得分: {score_正常:.4f}")
if score_垃圾 > score_正常:
print("预测:这是一封垃圾邮件。")
else:
print("预测:这是一封正常邮件。")
角色二:模型推断与学习 —— 寻找最可能的解释
如何从数据中找到那个最有可能生成这些数据的概率模型(即学习模型参数)?这里有两个核心思想:
1. 最大似然估计 核心思想:寻找能使观测到当前数据的概率(似然度)最大化的模型参数。 比喻:侦探破案。侦探会问:"在哪种作案动机和方式下,最有可能产生我们目前看到的所有现场痕迹?" MLE 就是在寻找这个"最可能"的假设。 优点:数据驱动,完全依赖数据。 潜在缺点:如果数据量少,可能过拟合;忽略先验知识。
2. 最大后验估计
核心思想:在最大似然的基础上,融入我们对参数的先验知识(P(假设)),寻找能使后验概率最大化的参数。
比喻:有经验的侦探破案。他不仅看现场痕迹(数据),还会结合已知的嫌疑人惯用手法(先验)来综合判断。
优点:能利用领域知识,在小数据集上表现更稳健,防止过拟合。
| 准则 | 全称 | 优化目标 | 核心思想 | 比喻 |
|---|---|---|---|---|
| MLE | 最大似然估计 | `P(数据 | 参数)` | 数据至上:什么参数最可能产生已观测数据? |
| MAP | 最大后验估计 | `P(参数 | 数据)` | 综合考量:结合先验知识和数据,什么参数最可信? |
角色三:预测与决策 —— 输出带信心的答案
一个优秀的模型不仅要给出预测,还要给出预测的不确定性。
- 分类任务:输出每个类别的概率(如:猫: 0.85, 狗: 0.12, 兔子: 0.03)。这比单纯输出"猫"包含了更多信息。我们可以根据概率阈值做决策(如:只有最高概率 > 0.8 时才采纳)。
- 回归任务:高级的回归模型(如概率回归、贝叶斯线性回归)可以预测一个分布(如高斯分布),而不仅仅是一个点估计值。它会告诉你:"预测价格是 100 万元,并且有 95% 的把握认为真实价格在 95 万到 105 万之间。"
第三部分:实践练习 —— 用概率思维解决一个简单问题
场景:一个简单的疾病检测。已知:
- 疾病在总人口中的发病率(先验概率)
P(病) = 0.001。 - 检测方法的准确率:如果真有病,检测为阳性的概率
P(阳|病) = 0.99(灵敏度)。如果没病,检测为阴性的概率P(阴|健康) = 0.99(特异度)。 - 问题:如果一个人检测结果是阳性,他真正患病的概率
P(病|阳)是多少?
直觉陷阱:很多人会认为高达 99%。让我们用贝叶斯定理来计算。
实例
P_disease = 0.001 # P(病)
P_positive_given_disease = 0.99 # P(阳|病)
P_negative_given_healthy = 0.99 # P(阴|健康)
# 计算派生概率
P_healthy = 1 - P_disease # P(健康)
P_positive_given_healthy = 1 - P_negative_given_healthy # P(阳|健康) = 1 - 特异度
# 计算全概率 P(阳)
# P(阳) = P(阳|病)*P(病) + P(阳|健康)*P(健康)
P_positive = (P_positive_given_disease * P_disease) + (P_positive_given_healthy * P_healthy)
# 应用贝叶斯定理计算 P(病|阳)
P_disease_given_positive = (P_positive_given_disease * P_disease) / P_positive
print(f"即使检测为阳性,真正患病的后验概率 P(病|阳) 仅为: {P_disease_given_positive:.2%}")
运行结果与思考:
你会惊讶地发现,P(病|阳) 只有大约 9%!这是因为疾病发病率很低(先验概率低),导致假阳性的数量远多于真阳性。这个例子深刻地展示了:
- 先验知识的重要性:忽略基础发病率会导致严重误判。
- 贝叶斯推理的力量:它迫使我们将所有相关信息(基础率、检测准确率)纳入考量。
- 概率思维的实用性:它能纠正我们直觉上的系统性偏差。
总结与进阶方向
概率思维的核心收获:
- 拥抱不确定性:世界是不确定的,模型的输出也应是概率化的。
- 贝叶斯是更新的哲学:通过
先验 + 数据 -> 后验的框架,持续用新证据修正认知。 - 决策需要概率:一个好的预测应该附带"信心分数",以支持风险可控的决策。
如果你想继续深入:
- 理论层面:学习概率图模型,它用图结构优雅地表示变量间的复杂概率依赖关系。
- 算法层面:探索变分推断和马尔可夫链蒙特卡洛方法,它们是求解复杂贝叶斯模型的利器。
- 应用层面:研究贝叶斯优化(用于超参数调优)、高斯过程(用于回归和优化)以及深度生成模型(如变分自编码器 VAE、扩散模型)。

点我分享笔记