统计学基础
在学习各种炫酷的算法之前,我们需要先打好一个至关重要的基础——统计学。
我们可以把统计学想象成机器学习的语言和工具箱,没有它,机器学习模型就像没有地图的探险家,无法理解数据、做出预测或评估自己的表现。
本文将为你系统性地介绍机器学习中必备的统计学核心概念,用通俗的语言和生动的例子,帮助你构建坚实的理论基础。
为什么机器学习需要统计学?
核心原因:机器学习本质上是从数据中学习规律,并用这个规律对未知情况进行预测或决策。而统计学,正是研究如何收集、分析、解释和呈现数据的科学。
- 数据理解:统计学帮助我们描述数据的基本特征(比如平均身高、收入分布),这是数据清洗和探索的第一步。
- 规律挖掘:它提供了从数据中推断出普遍规律(模型)的方法,并告诉我们这个规律有多可靠。
- 预测与评估:统计学理论支撑着我们如何用模型进行预测,以及如何客观地评估一个模型的好坏(是瞎猜还是真懂?)。
- 不确定性量化:现实世界充满噪音,统计学让我们能够度量预测中的不确定性(例如,"我有95%的把握认为明天会下雨")。
简单来说,统计学是机器学习的理论基石,让智能从玄学变为科学。
核心概念一:描述性统计
描述性统计就像给数据拍快照和体检报告,用几个关键指标来概括数据集的全貌。这是任何数据分析项目的起点。
1. 集中趋势:数据围绕哪里聚集?
这组指标告诉我们数据的中心或典型值在哪里。
| 指标 | 解释(比喻) | 计算公式(简述) | 特点与用途 |
|---|---|---|---|
| 均值 | 所有数据的算术平均值。 好比"平均工资"。 |
总和 / 数据个数 |
最常用,但对极端值(如亿万富翁)非常敏感,容易"被平均"。 |
| 中位数 | 将数据从小到大排序后,正中间的那个值。 好比"工资中位数"。 |
排序后取中间位置的值 | 稳健,不受极端值影响,能更好地反映普通情况。 |
| 众数 | 数据中出现次数最多的值。 好比店里最畅销的鞋码。 |
出现频率最高的值 | 适用于分类数据,或寻找最普遍的类别。 |
示例:一个部门5名员工的月薪(单位:千元)为:[30, 35, 40, 45, 200](老板也在其中)。
- 均值 = (30+35+40+45+200)/5 = 70。这个值因为老板的200而虚高,不能代表员工收入。
- 中位数 = 排序后的第三个数 40。这个值更能代表该部门"典型"员工的收入。
- 众数 = 所有值只出现一次,所以没有众数。
2. 离散程度:数据有多分散?
光知道中心不够,我们还需要知道数据是紧密围绕中心,还是散落四处。离散程度衡量数据的波动性或多样性。
| 指标 | 解释(比喻) | 计算公式(简述) | 特点与用途 |
|---|---|---|---|
| 方差 | 每个数据点与均值距离的平方的平均值。 | Σ(每个值 - 均值)² / (n-1) |
衡量总体离散程度,单位是原单位的平方。 |
| 标准差 | 方差的正平方根。 好比"平均波动幅度"。 |
√方差 |
最常用,单位与原数据一致,直观反映波动大小。值越大,数据越分散。 |
| 极差 | 最大值与最小值的差。 "工资跨度"。 |
最大值 - 最小值 |
计算简单,但只由两个极端值决定,容易受异常值影响。 |
接上例:计算员工薪资的标准差(均值用40估算更合理)。
- 计算方差:
[(30-40)² + (35-40)² + (40-40)² + (45-40)² + (200-40)²] / 4 ≈ 5875 - 标准差 =
√5875 ≈ 76.65。这个巨大的标准差(76.65)远大于均值(40),强烈提示数据中存在极端异常值(老板的200),需要进一步分析。
3. 数据分布与可视化
数字指标是抽象的,图表能让我们直观"看到"数据。
- 直方图:展示数据在不同区间(桶)内的频率分布。可以看出数据是单峰还是多峰,是否对称。
- 箱线图:用一个"箱子"和"触须"展示数据的最小值、第一四分位数(Q1)、中位数(Q2)、第三四分位数(Q3)、最大值,是识别异常值的利器。
实例
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
# 员工薪资数据,包含一个异常值
salaries = np.array([30, 35, 40, 45, 200])
employee_names = ['Alice', 'Bob', 'Charlie', 'Diana', 'Boss']
plt.figure(figsize=(8, 5))
# 创建箱线图
sns.boxplot(y=salaries)
plt.title('Department Salary Distribution (Boxplot)')
plt.ylabel('Salary (k)')
plt.grid(axis='y', linestyle='--', alpha=0.7)
# 标注出异常值对应的点
for i, (name, salary) in enumerate(zip(employee_names, salaries)):
if salary > 45 + 1.5 * (45-35): # 简单异常值判断规则
plt.annotate(f'{name}: {salary}', xy=(0, salary), xytext=(0.2, salary),
arrowprops=dict(facecolor='red', shrink=0.05))
plt.show()
代码解释:
sns.boxplot()绘制箱线图。箱体从 Q1 到 Q3,中间线是中位数。- 箱线图的"触须"通常延伸到 1.5 倍四分位距(IQR = Q3 - Q1)以内的最远数据点,之外的点被视为异常值并用点单独标出。图中
200这个点被清晰地识别为异常值。
核心概念二:概率与分布
如果说描述性统计是看历史,那么概率就是预测未来。它量化了某件事情发生的可能性。
1. 基本概率
- 概率 P(A):事件 A 发生的可能性,范围在 0(不可能)到 1(必然)之间。
- 条件概率 P(A|B):在事件 B 已经发生的条件下,事件 A 发生的概率。这是理解很多机器学习算法(如朴素贝叶斯)的关键。
- 公式:
P(A|B) = P(A 且 B) / P(B)
- 公式:
2. 概率分布
描述一个随机变量取各种可能值的概率规律。机器学习中最重要的是:
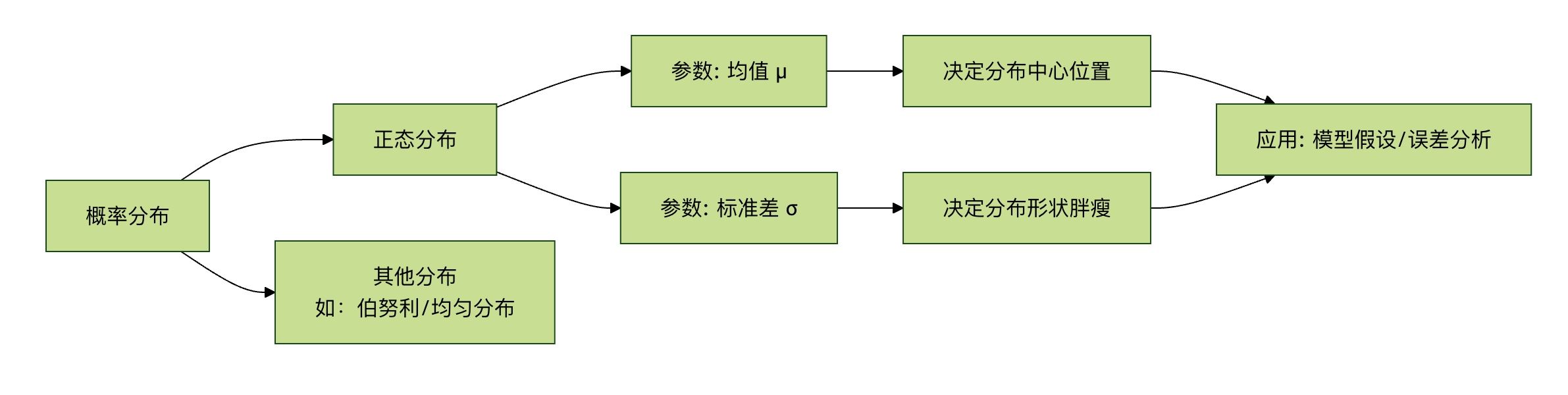
- 正态分布(高斯分布):
- 形状:著名的"钟形曲线",左右对称。
- 参数:由**均值(μ)**决定中心位置,**标准差(σ)**决定曲线的"胖瘦"(分散程度)。
- 重要性:自然界和社会科学中大量现象都近似服从正态分布(如身高、测量误差)。中心极限定理指出,多个独立随机变量之和趋向于正态分布,这使其成为统计推断的基石。
- 68-95-99.7 法则:数据落在均值±1σ、±2σ、±3σ范围内的概率分别约为68%、95%、99.7%。
核心概念三:推断性统计
这是统计学的"升级版",目标是从样本数据推断总体的性质。机器学习中,我们总在用有限的数据(样本)训练模型,希望它能在无限的真实世界(总体)中表现良好。
1. 中心极限定理
核心思想:无论总体是什么分布,当我们从总体中抽取大量独立的随机样本,并计算每个样本的均值,这些样本均值的分布会趋近于一个正态分布。
对机器学习的意义:这为我们利用正态分布的性质来对模型参数(如均值)进行假设检验和构建置信区间提供了理论依据。即使我们不知道总体的真实分布,也能对基于样本得到的估计值进行可靠性分析。
2. 假设检验
用于判断一个关于总体的假设(如"新药无效")是否被样本数据所支持。
- 零假设(H0):通常表示"没有效果"、"没有差异"(默认立场)。
- 备择假设(H1):我们希望证实的假设(如"新药有效")。
- P 值:在零假设成立的前提下,观察到当前样本数据(或更极端数据)的概率。
- 如何判断:如果 P 值很小(通常 < 0.05),意味着在 H0 下当前情况极难发生,于是我们有足够证据拒绝 H0,接受 H1。
- 显著性水平(α):判断 P 值是否"足够小"的阈值,常设为 0.05。
机器学习中的应用:用于特征选择,判断某个特征与目标变量之间是否存在统计上显著的相关性,而非偶然关联。
3. 相关性与因果性
这是数据分析中最容易混淆,也最重要的概念之一。
- 相关性:衡量两个变量同时变化的趋势。常用**相关系数(-1 到 1)**表示。
- 1:完全正相关(同增同减)。
- -1:完全负相关(一增一减)。
- 0:无线性相关。
- 因果性:指一个变量(因)的变化直接导致另一个变量(果)的变化。
关键区别:相关性不等于因果性!
- 经典谬误:夏天冰淇淋销量和溺水人数高度正相关。但这并不意味着吃冰淇淋导致溺水。其共同原因(混杂变量)是天气炎热。
- 对机器学习的启示:机器学习模型(尤其是预测模型)善于发现相关性,但无法自行确定因果性。将模型发现的强相关关系误认为是因果关系,是实践中常见的错误。建立因果模型需要更严谨的实验设计(如随机对照试验)或特殊的因果推断方法。
实践练习:用 Python 进行基础统计分析
让我们用 Python 和著名的 pandas、seaborn 库,对一个真实数据集进行简单的描述性和探索性统计分析。
实例
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
# 1. 加载数据集(这里使用 seaborn 自带的'tips'小费数据集)
df = sns.load_dataset('tips')
print("数据集前5行:")
print(df.head())
print(f"\n数据集形状:{df.shape}") # 查看行数和列数
print("\n基本信息:")
print(df.info())
print("\n描述性统计:")
print(df.describe())
# 2. 探索数值型变量:总账单(total_bill)和小费(tip)
print(f"\n总账单的均值:{df['total_bill'].mean():.2f}")
print(f"总账单的中位数:{df['total_bill'].median():.2f}")
print(f"总账单的标准差:{df['total_bill'].std():.2f}")
print(f"小费与总账单的相关系数:{df['tip'].corr(df['total_bill']):.3f}")
# 3. 可视化
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
# 3.1 总账单的直方图与密度估计
sns.histplot(df['total_bill'], kde=True, ax=axes[0, 0])
axes[0, 0].set_title('Distribution of Total Bill')
axes[0, 0].axvline(df['total_bill'].mean(), color='red', linestyle='--', label=f'Mean: {df["total_bill"].mean():.1f}')
axes[0, 0].axvline(df['total_bill'].median(), color='green', linestyle='--', label=f'Median: {df["total_bill"].median():.1f}')
axes[0, 0].legend()
# 3.2 小费与总账单的散点图(看相关性)
sns.scatterplot(data=df, x='total_bill', y='tip', hue='time', ax=axes[0, 1])
axes[0, 1].set_title('Tip vs Total Bill (Colored by Meal Time)')
# 3.3 按性别分组的小费箱线图(比较组间差异)
sns.boxplot(data=df, x='sex', y='tip', ax=axes[1, 0])
axes[1, 0].set_title('Tip Amount by Gender')
# 3.4 吸烟与否的账单均值柱状图
bill_by_smoker = df.groupby('smoker')['total_bill'].mean().reset_index()
sns.barplot(data=bill_by_smoker, x='smoker', y='total_bill', ax=axes[1, 1])
axes[1, 1].set_title('Average Total Bill by Smoking Status')
for index, row in bill_by_smoker.iterrows():
axes[1, 1].text(index, row['total_bill']+0.5, f"{row['total_bill']:.1f}", ha='center')
plt.tight_layout()
plt.show()
练习任务:
运行代码:在你的 Python 环境中运行上述代码,观察输出和图表。
解读结果:
- 从描述性统计表中,你能说出总账单的大致范围和中位数吗?
- 小费和总账单是正相关还是负相关?从散点图中能看出来吗?
- 从箱线图看,男性和女性给的小费中位数有显著差异吗?
提出假设:基于"吸烟与否的账单均值"柱状图,你能提出一个可以用于假设检验的零假设吗?(例如:H0: 吸烟者和非吸烟者的平均账单没有差异)。

点我分享笔记