前向传播与反向传播
在深度学习中,前向传播与反向传播是支撑其运转的两大核心支柱。它们如同一个硬币的两面,共同构成了神经网络从学习到应用的完整闭环,透彻理解这两个过程,是打开深度学习大门的第一把钥匙。
本文将带你一步步拆解这两个看似复杂的概念,用清晰的逻辑和生动的比喻,让你不仅知其然,更知其所以然。
什么是前向传播与反向传播?
在深入细节之前,让我们先建立一个宏观的认知。
想象一下,你正在教一个孩子识别猫和狗。你给他看一张图片(输入),他根据自己大脑中已有的知识(网络参数,即权重和偏置)进行判断,然后告诉你这是猫(输出)。这个看图片 -> 大脑处理 -> 给出答案的过程,就是前向传播。
但孩子的判断可能出错。你告诉他:不对,这是狗。这个正确答案与孩子答案之间的差异,就是误差。孩子需要根据这个误差,回头去反思:我大脑里的哪些知识(参数)导致了这次误判?我应该如何调整它们,下次才能认对?这个根据误差,从后往前调整知识的过程,就是反向传播。
在神经网络中:
- 前向传播:数据从输入层,经过隐藏层,最终到达输出层,并产生预测结果的过程。这是一个推理过程。
- 反向传播:根据前向传播产生的预测结果与真实值之间的误差,从输出层开始,反向逐层计算每个参数(权重和偏置)对总误差的"贡献"大小(即梯度),并据此更新参数。这是一个学习过程。
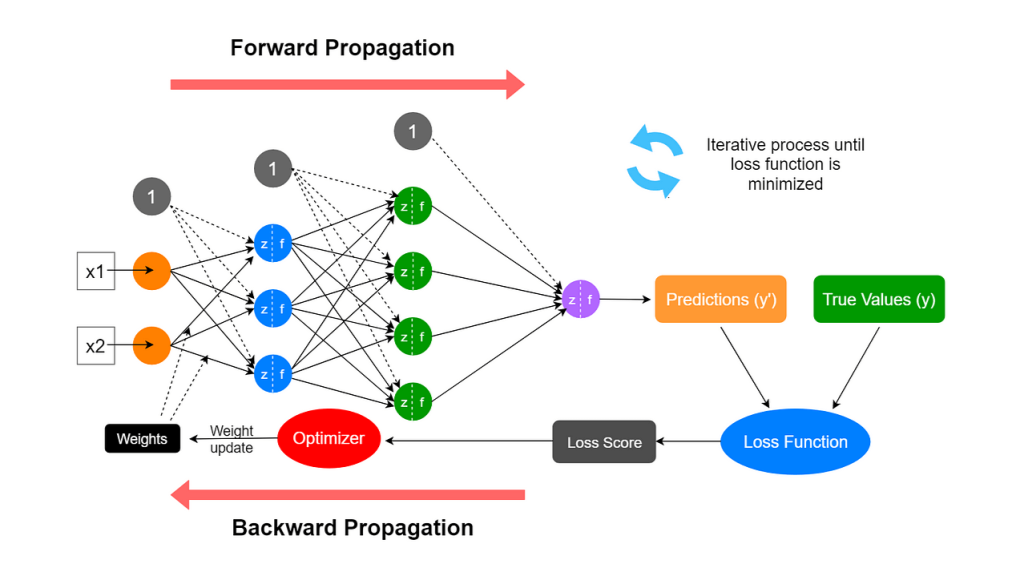
它们的关系可以用一个简单的学习循环图来表示:
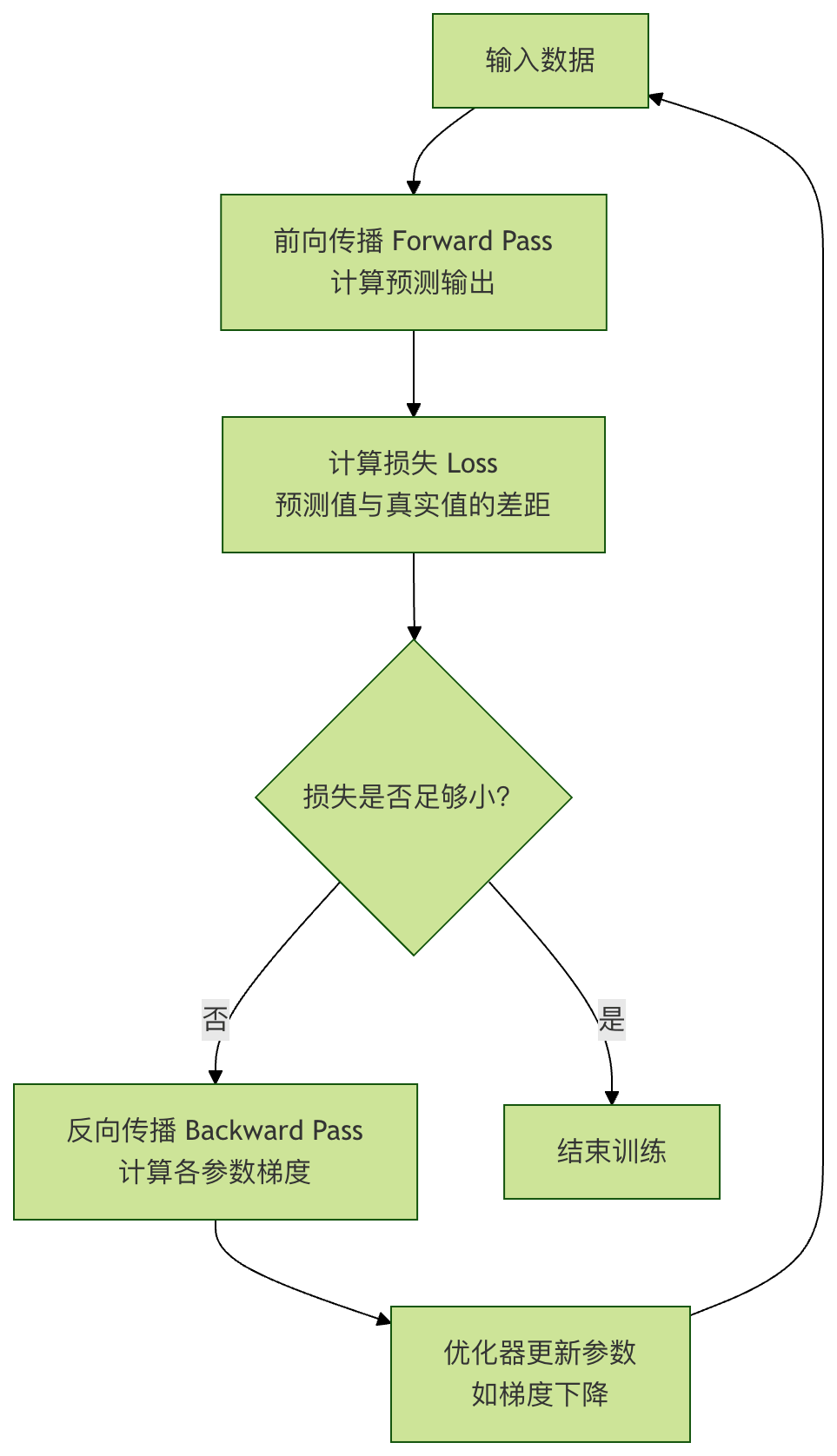
前向传播:神经网络的推理之路
前向传播是神经网络进行预测的前向通道。让我们通过一个最简单的三层神经网络(输入层、一个隐藏层、输出层)来理解它。
核心概念与计算
假设我们要预测房价,输入是房屋面积 x。我们的微型网络结构如下:
- 输入层:一个神经元,接收
x。 - 隐藏层:一个神经元,拥有权重
w1和偏置b1。 - 输出层:一个神经元,拥有权重
w2和偏置b2,输出预测房价y_pred。
前向传播的计算分为两步:
1、隐藏层计算:输入 x 与权重 w1、偏置 b1 结合,然后通过一个激活函数(例如Sigmoid,记作 σ),产生隐藏层输出 a1。
z1 = w1 * x + b1 a1 = σ(z1) = 1 / (1 + exp(-z1))
z1是线性变换结果。a1是经过非线性激活后的输出,这赋予了网络学习复杂模式的能力。
2、输出层计算:隐藏层输出 a1 作为输入,与输出层的权重 w2、偏置 b2 结合,产生最终预测 y_pred。这里为了简化,假设输出层不使用激活函数(即线性输出)。
y_pred = w2 * a1 + b2
代码示例:手动实现前向传播
实例
def sigmoid(x):
"""Sigmoid激活函数"""
return 1 / (1 + np.exp(-x))
# 初始化网络参数(通常随机初始化,这里为演示指定值)
w1, b1 = 2.0, -1.0 # 隐藏层参数
w2, b2 = 1.5, 0.5 # 输出层参数
def forward_pass(x):
"""执行一次前向传播"""
# 隐藏层计算
z1 = w1 * x + b1
a1 = sigmoid(z1) # 应用激活函数
# 输出层计算
y_pred = w2 * a1 + b2 # 线性输出
# 返回中间结果和最终预测,便于后续理解
return {'z1': z1, 'a1': a1, 'y_pred': y_pred}
# 假设房屋面积为 3(单位:百平方米)
x_input = 3.0
result = forward_pass(x_input)
print(f"输入 x = {x_input}")
print(f"隐藏层线性输出 z1 = w1*x + b1 = {result['z1']:.4f}")
print(f"隐藏层激活输出 a1 = sigmoid(z1) = {result['a1']:.4f}")
print(f"最终预测房价 y_pred = w2*a1 + b2 = {result['y_pred']:.4f}")
输出示例:
输入 x = 3.0 隐藏层线性输出 z1 = w1*x + b1 = 5.0000 隐藏层激活输出 a1 = sigmoid(z1) = 0.9933 最终预测房价 y_pred = w2*a1 + b2 = 1.9899
这个 y_pred 就是网络对面积为3的房屋的预测价格。但显然,这个预测值(基于我们随便设定的参数)很可能与真实房价相差甚远。如何衡量这个差距并改进呢?这就需要损失函数和接下来的反向传播。
损失函数:好坏的衡量标尺
在反向传播开始之前,我们必须先量化预测值 y_pred 与真实值 y_true 之间的差距。这就是损失函数的作用。
常用损失函数:
- 均方误差:适用于回归问题(如预测房价、温度)。
Loss = (1/N) * Σ (y_true - y_pred)^2 - 交叉熵损失:适用于分类问题(如图像分类、垃圾邮件识别)。
以均方误差为例,对于单个样本:
Loss = (y_true - y_pred)^2
我们的目标就是通过调整 w1, b1, w2, b2,让这个 Loss 值尽可能小。
反向传播:神经网络的学习引擎
反向传播是深度学习的学习算法核心。其本质是链式法则在神经网络中的高效应用。目标是计算损失函数 L 对每个参数(w1, b1, w2, b2)的偏导数(梯度),即 ∂L/∂w1, ∂L/∂b1 等。这些梯度指明了为了减小损失,每个参数应该朝哪个方向、以多大的幅度调整。
理解梯度:下山的方向与步幅
想象你蒙着眼站在一座山上(损失曲面),目标是找到山谷的最低点(最小损失)。你每走一步前,都需要用脚感受一下周围最陡的下坡方向。这个最陡的下坡方向就是梯度。反向传播就是帮你精确计算出脚下每一个点(对应每一组参数)的梯度。
反向传播计算步骤(链式求导)
我们继续沿用前面的微型网络,并假设真实房价 y_true = 2.5,损失函数为均方误差 L = (y_true - y_pred)^2。
反向传播从输出层开始,反向逐层计算梯度:
计算输出层参数的梯度
- 损失
L对预测值y_pred的梯度:∂L/∂y_pred = -2 * (y_true - y_pred) - 因为
y_pred = w2 * a1 + b2,所以:∂L/∂w2 = (∂L/∂y_pred) * (∂y_pred/∂w2) = (∂L/∂y_pred) * a1∂L/∂b2 = (∂L/∂y_pred) * (∂y_pred/∂b2) = (∂L/∂y_pred) * 1
计算隐藏层参数的梯度
- 首先,需要损失
L对隐藏层输出a1的梯度。a1通过y_pred影响L:∂L/∂a1 = (∂L/∂y_pred) * (∂y_pred/∂a1) = (∂L/∂y_pred) * w2 - 然后,
a1 = σ(z1),Sigmoid函数的导数σ'(z) = σ(z)*(1-σ(z))。 - 最后,计算
L对隐藏层参数w1,b1的梯度:∂L/∂w1 = (∂L/∂a1) * (∂a1/∂z1) * (∂z1/∂w1) = (∂L/∂a1) * σ'(z1) * x∂L/∂b1 = (∂L/∂a1) * (∂a1/∂z1) * (∂z1/∂b1) = (∂L/∂a1) * σ'(z1) * 1
代码示例:手动实现反向传播
实例
y_true = 2.5
y_pred = result['y_pred']
a1 = result['a1']
z1 = result['z1']
x = x_input
print(f"真实值 y_true = {y_true}")
print(f"预测值 y_pred = {y_pred:.4f}")
print(f"初始损失 Loss = {(y_true - y_pred)**2:.4f}")
print("\n--- 开始反向传播计算梯度 ---")
# 1. 计算损失对y_pred的梯度
dL_dy_pred = -2 * (y_true - y_pred)
print(f"梯度 ∂L/∂y_pred = -2*(y_true - y_pred) = {dL_dy_pred:.4f}")
# 2. 计算输出层参数 w2, b2 的梯度
dL_dw2 = dL_dy_pred * a1
dL_db2 = dL_dy_pred * 1
print(f"梯度 ∂L/∂w2 = (∂L/∂y_pred) * a1 = {dL_dw2:.4f}")
print(f"梯度 ∂L/∂b2 = (∂L/∂y_pred) * 1 = {dL_db2:.4f}")
# 3. 计算损失对隐藏层输出a1的梯度
dL_da1 = dL_dy_pred * w2
print(f"梯度 ∂L/∂a1 = (∂L/∂y_pred) * w2 = {dL_da1:.4f}")
# 4. 计算Sigmoid函数的导数在z1处的值
def sigmoid_derivative(x):
"""Sigmoid函数的导数"""
s = sigmoid(x)
return s * (1 - s)
sigma_prime_z1 = sigmoid_derivative(z1)
print(f"Sigmoid导数 σ'(z1) = σ(z1)*(1-σ(z1)) = {sigma_prime_z1:.4f}")
# 5. 计算隐藏层参数 w1, b1 的梯度
dL_dw1 = dL_da1 * sigma_prime_z1 * x
dL_db1 = dL_da1 * sigma_prime_z1 * 1
print(f"梯度 ∂L/∂w1 = (∂L/∂a1) * σ'(z1) * x = {dL_dw1:.4f}")
print(f"梯度 ∂L/∂b1 = (∂L/∂a1) * σ'(z1) * 1 = {dL_db1:.4f}")
输出示例:
真实值 y_true = 2.5 预测值 y_pred = 1.9899 初始损失 Loss = 0.2602 --- 开始反向传播计算梯度 --- 梯度 ∂L/∂y_pred = -2*(y_true - y_pred) = -1.0202 梯度 ∂L/∂w2 = (∂L/∂y_pred) * a1 = -1.0134 梯度 ∂L/∂b2 = (∂L/∂y_pred) * 1 = -1.0202 梯度 ∂L/∂a1 = (∂L/∂y_pred) * w2 = -1.5303 Sigmoid导数 σ'(z1) = σ(z1)*(1-σ(z1)) = 0.0066 梯度 ∂L/∂w1 = (∂L/∂a1) * σ'(z1) * x = -0.0304 梯度 ∂L/∂b1 = (∂L/∂a1) * σ'(z1) * 1 = -0.0101
现在,我们得到了所有参数的梯度。这些负值意味着,如果增加这些参数的值,损失会增大(因为梯度方向是上升方向)。为了减小损失,我们应该沿着梯度的反方向调整参数。
参数更新:梯度下降
拿到梯度后,我们使用梯度下降算法来更新参数:
参数 = 参数 - 学习率 * 该参数的梯度
其中,学习率是一个非常重要的超参数,它控制了每次参数更新的步长。步长太小,学习缓慢;步长太大,可能无法收敛甚至发散。
代码示例:应用梯度下降更新参数
实例
# 更新参数
w1_new = w1 - learning_rate * dL_dw1
b1_new = b1 - learning_rate * dL_db1
w2_new = w2 - learning_rate * dL_dw2
b2_new = b2 - learning_rate * dL_db2
print("--- 更新后的参数 ---")
print(f"w1: {w1:.4f} -> {w1_new:.4f}")
print(f"b1: {b1:.4f} -> {b1_new:.4f}")
print(f"w2: {w2:.4f} -> {w2_new:.4f}")
print(f"b2: {b2:.4f} -> {b2_new:.4f}")
# 用新参数做一次前向传播,验证损失是否减小
def forward_pass_with_params(x, w1, b1, w2, b2):
z1 = w1 * x + b1
a1 = sigmoid(z1)
y_pred = w2 * a1 + b2
return y_pred
y_pred_new = forward_pass_with_params(x_input, w1_new, b1_new, w2_new, b2_new)
loss_new = (y_true - y_pred_new)**2
print(f"\n用新参数预测: y_pred_new = {y_pred_new:.4f}")
print(f"更新后的损失 New Loss = {loss_new:.4f}")
print(f"损失变化: {loss_new - (y_true-y_pred)**2:.4f} (负值表示损失减小)")
输出示例:
--- 更新后的参数 --- w1: 2.0000 -> 2.0030 b1: -1.0000 -> -0.9990 w2: 1.5000 -> 1.6013 b2: 0.5000 -> 0.6020 用新参数预测: y_pred_new = 2.1933 更新后的损失 New Loss = 0.0940 损失变化: -0.1662 (负值表示损失减小)
太好了!经过一次前向传播 -> 计算损失 -> 反向传播 -> 梯度下降更新的完整循环,我们的预测值 y_pred 从 1.99 更接近真实值 2.5,损失也从 0.260 下降到了 0.094。将这个循环重复成千上万次(在大量数据上),神经网络就能学习到有效的参数,做出准确的预测。
实践练习:巩固你的理解
现在,是时候动手巩固所学知识了。
练习 1:扩展网络
修改上面的代码,将隐藏层神经元增加到2个。你需要初始化 w1 为一个形状为 (2,) 的数组(两个权重),b1 为 (2,) 的数组。相应地调整前向传播和反向传播的计算。观察网络能力的变化。
练习 2:更换激活函数
将Sigmoid激活函数替换为ReLU函数(f(x) = max(0, x))。你需要重新推导并实现ReLU的导数(f'(x) = 1 if x>0 else 0)。比较使用不同激活函数时,训练过程有何不同。
练习 3:实现一个训练循环
编写一个完整的训练循环,在某个简单数据集(例如,自己构造 y = 2x + 1 + 噪声 的数据)上,训练一个微型网络去拟合它。设置迭代次数(epoch),在每次迭代后打印损失,观察损失是否随着训练持续下降。
练习 4:理解学习率的影响
在练习3的基础上,尝试不同的 learning_rate(如 0.01, 0.1, 0.5, 1.0)。观察学习率过大或过小时,损失曲线的变化(是震荡、发散还是收敛缓慢),深刻理解学习率作为步幅的重要性。
总结
前向传播与反向传播是神经网络学习的核心动态:
- 前向传播是推理路径,它利用当前参数将输入映射为输出,并计算当前表现的得分(损失)。
- 反向传播是学习算法,它利用链式法则,高效地计算出损失函数对网络中每一个参数的梯度,指明了参数优化的方向。
- 梯度下降是优化策略,它根据反向传播提供的梯度,以学习率为步长,实际更新参数,使网络的表现逐步改善。

点我分享笔记