损失函数与梯度
本章节我们将一起探索两个至关重要的核心概念:损失函数 和 梯度,它们是机器学习算法能够学习和改进的基石。
想象一下,你在学习投篮,每次投球后,你都会观察球是进了、偏左了还是偏右了。这个观察结果与完美进球之间的差距,就是你的损失。而为了下次投得更准,你会根据这次偏差的方向和大小来调整你的姿势和力度,这个调整的方向和大小就类似于梯度。
在机器学习中,模型就是那个学习者,损失函数衡量它的错误程度,而梯度则告诉它如何改进。理解它们,你就掌握了机器学习如何工作的核心逻辑。
一、 损失函数:模型的成绩单
1.1 什么是损失函数?
损失函数,有时也叫代价函数或目标函数,是一个用来量化模型预测值与真实值之间差异的函数。
- 核心作用:它给模型的预测表现打了一个具体的"分数"。这个分数越低,说明模型预测得越准确;分数越高,说明预测误差越大。
- 类比理解:就像考试一样,损失函数的"分数"就是模型的考试成绩。我们的终极目标就是通过"学习"(调整模型参数),让这个分数(损失)越来越低。
1.2 常见损失函数举例
不同的任务需要使用不同的评分标准,以下是两个最基础的损失函数:
均方误差 - 适用于回归问题(预测连续值,如房价、温度)
均方误差计算的是所有样本的预测值与真实值之差的平方的平均值。
公式: MSE = (1/n) * Σ(真实值ᵢ - 预测值ᵢ)²
n:样本数量Σ:求和符号真实值ᵢ:第 i 个样本的真实值预测值ᵢ:模型对第 i 个样本的预测值
特点:由于使用了平方,它对较大的误差惩罚更重(误差为 2 时,平方后贡献为 4;误差为 10 时,平方后贡献高达 100)。
代码示例:
实例
# 假设我们有 5 个样本的真实值和预测值
y_true = np.array([3, -0.5, 2, 7, 4]) # 真实值
y_pred = np.array([2.5, 0.0, 2, 8, 5]) # 预测值
# 手动计算 MSE
n = len(y_true)
squared_errors = (y_true - y_pred) ** 2 # 计算每个样本的平方误差
mse_manual = np.sum(squared_errors) / n # 求和并取平均
print(f"手动计算的 MSE: {mse_manual}")
# 使用 sklearn 库函数验证
from sklearn.metrics import mean_squared_error
mse_sklearn = mean_squared_error(y_true, y_pred)
print(f"Sklearn 计算的 MSE: {mse_sklearn}")
交叉熵损失 - 适用于分类问题(预测类别,如图片是猫还是狗)
交叉熵衡量的是模型预测的概率分布与真实的概率分布之间的差异。在二分类中,真实分布通常是 [1, 0](是类别 A)或 [0, 1](是类别 B)。
二分类公式(对数损失):
Log Loss = - (1/n) * Σ [真实值ᵢ * log(预测概率ᵢ) + (1 - 真实值ᵢ) * log(1 - 预测概率ᵢ)]
直观理解:当真实标签为 1 时,我们希望模型预测的概率也接近 1。如果此时模型预测了一个很低的概率(比如 0.1),那么 log(0.1) 会是一个很大的负数,再乘以前面的负号,就会导致损失值变得很大,表示惩罚很重。
代码示例:
实例
from sklearn.metrics import log_loss
# 二分类示例:真实标签(1代表"是",0代表"否")
y_true_binary = np.array([1, 0, 0, 1]) # 真实类别:是,否,否,是
# 模型预测为"是"这个类别的概率
y_pred_prob = np.array([0.9, 0.1, 0.2, 0.8]) # 预测概率:0.9, 0.1, 0.2, 0.8
# 使用 sklearn 计算交叉熵损失(对数损失)
ce_loss = log_loss(y_true_binary, y_pred_prob)
print(f"交叉熵损失 (Log Loss): {ce_loss}")
二、 梯度:指引优化方向的"指南针"
现在我们知道了如何给模型打分(损失函数),接下来最关键的问题是:模型如何根据这个分数来改进自己? 答案就是通过梯度。
2.1 什么是梯度?
在机器学习中,模型通常由许多参数(或叫权重)构成。我们可以把损失函数 L 看作是所有这些参数的函数:L(w1, w2, ..., wn)。
- 梯度 就是损失函数对每个参数的偏导数所构成的向量。
- 数学表示:
∇L = [∂L/∂w1, ∂L/∂w2, ..., ∂L/∂wn] - 核心意义:
- 方向:梯度向量所指的方向,是损失函数在该点上升最快的方向。
- 大小:每个偏导数的绝对值大小,表示损失函数对该参数变化的敏感度。
2.2 为什么梯度能指引优化?
我们的目标是最小化损失函数。既然梯度指向了损失上升最快的方向,那么它的反方向 -∇L 自然就是损失下降最快的方向。
优化过程(梯度下降)可以形象地理解为:
你站在一座山谷(损失曲面)的某个山坡上,蒙着眼睛想要走到谷底(损失最小点)。你每走一步前,都用脚感受一下四周哪个方向最陡峭(计算梯度),然后朝着最陡峭的下坡方向(负梯度方向)迈出一步(更新参数)。重复这个过程,你最终就能到达谷底。
这个过程可以用下面的流程图概括:
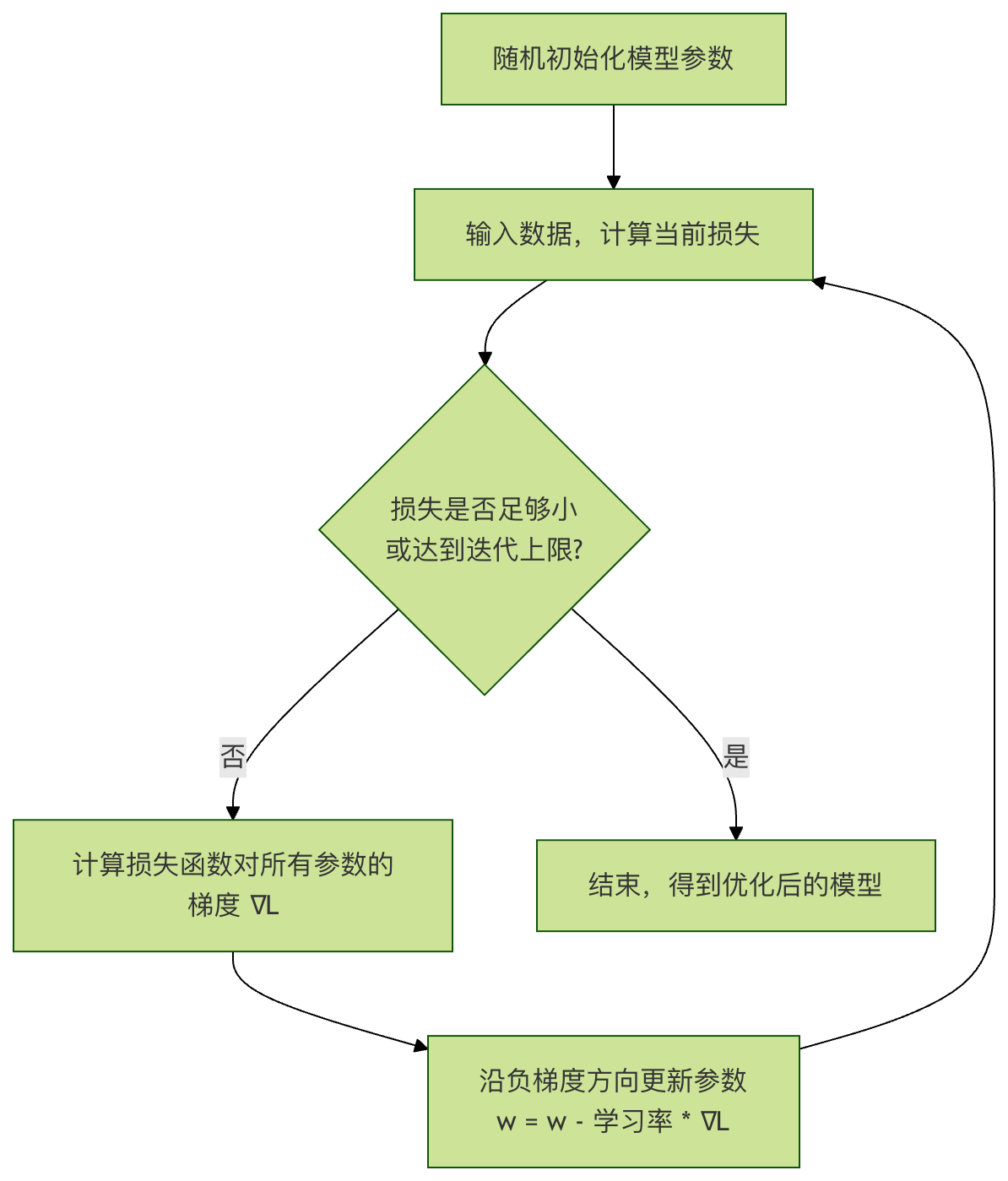
2.3 梯度下降的简单示例
让我们用一个最简单的例子——只有一个参数 w 的线性模型,来演示梯度下降。
假设我们的损失函数是 L(w) = w²。显然,当 w = 0 时,损失最小。
- 梯度计算:
∇L = dL/dw = 2w - 参数更新公式:
w_new = w_old - η * (2 * w_old)η是学习率,控制每一步迈多大。
实例
import matplotlib.pyplot as plt
# 定义损失函数 L(w) = w^2
def loss(w):
return w ** 2
# 定义梯度 dL/dw = 2*w
def gradient(w):
return 2 * w
# 梯度下降算法
def gradient_descent(start_w, learning_rate, iterations):
w = start_w
w_history = [w] # 记录 w 的变化历史
loss_history = [loss(w)] # 记录损失的变化历史
for i in range(iterations):
grad = gradient(w) # 计算当前点的梯度
w = w - learning_rate * grad # 沿负梯度方向更新参数
w_history.append(w)
loss_history.append(loss(w))
return w_history, loss_history
# 执行梯度下降:从 w=5 开始,学习率 0.1,迭代 20 次
w_start = 5.0
lr = 0.1
iters = 20
w_hist, loss_hist = gradient_descent(w_start, lr, iters)
print(f"初始 w: {w_hist[0]:.4f}, 初始损失: {loss_hist[0]:.4f}")
print(f"最终 w: {w_hist[-1]:.4f}, 最终损失: {loss_hist[-1]:.4f}")
# 可视化优化过程
plt.figure(figsize=(12, 4))
# 图1:损失函数曲线及优化路径
plt.subplot(1, 2, 1)
w_vals = np.linspace(-6, 6, 100)
plt.plot(w_vals, loss(w_vals), label='L(w) = w²')
plt.scatter(w_hist, loss_hist, c='red', s=20, label='Gradient Descent Steps')
plt.plot(w_hist, loss_hist, 'r--', alpha=0.5)
plt.xlabel('Parameter w')
plt.ylabel('Loss L(w)')
plt.title('Gradient Descent on L(w)=w²')
plt.legend()
plt.grid(True)
# 图2:损失值随迭代次数的下降曲线
plt.subplot(1, 2, 2)
plt.plot(range(len(loss_hist)), loss_hist, 'b-o')
plt.xlabel('Iteration')
plt.ylabel('Loss')
plt.title('Loss Reduction Over Iterations')
plt.grid(True)
plt.tight_layout()
plt.show()
运行这段代码,你会看到:
- 左边的图展示了参数
w如何从 5.0 开始,一步步"滚下"抛物线,最终接近最小值点 0。 - 右边的图展示了损失值如何随着迭代次数的增加而迅速下降。
三、 核心要点与联系总结
| 概念 | 比喻 | 核心作用 | 关键点 |
|---|---|---|---|
| 损失函数 | 成绩单/误差测量尺 | 定量评估模型预测的好坏。 | 1. 不同类型任务(回归、分类)使用不同的损失函数。 2. 损失值越小,模型性能越好。 |
| 梯度 | 指南针/最陡下坡方向 | 指出为了最快降低损失,每个模型参数应该如何调整。 | 1. 是损失函数对所有参数的偏导数向量。 2. 负梯度方向是损失下降最快的方向。 |
| 梯度下降 | 蒙眼下山法 | 利用梯度信息,迭代地更新参数以最小化损失。 | 1. 学习率是关键超参数,太小则学习慢,太大可能无法收敛。 2. 是大多数机器学习模型训练的底层优化算法。 |
它们之间的关系链是: 模型做出预测 → 损失函数计算误差 → 计算误差相对于各参数的梯度 → 沿负梯度方向更新参数 → 模型改进 → 重复...

点我分享笔记