聚类
想象一下,你走进一个巨大的图书馆,里面所有的书都杂乱无章地堆在地上,你的任务不是去读每一本书(那太费时间了),而是根据书的主题,比如:科幻小说、历史传记、烹饪食谱,将它们分成几堆。在这个过程中,你并没有一个现成的分类清单告诉你哪本书属于哪一类,你完全是依靠书的内容、封面、厚度等特征,自发地发现了这些群体。
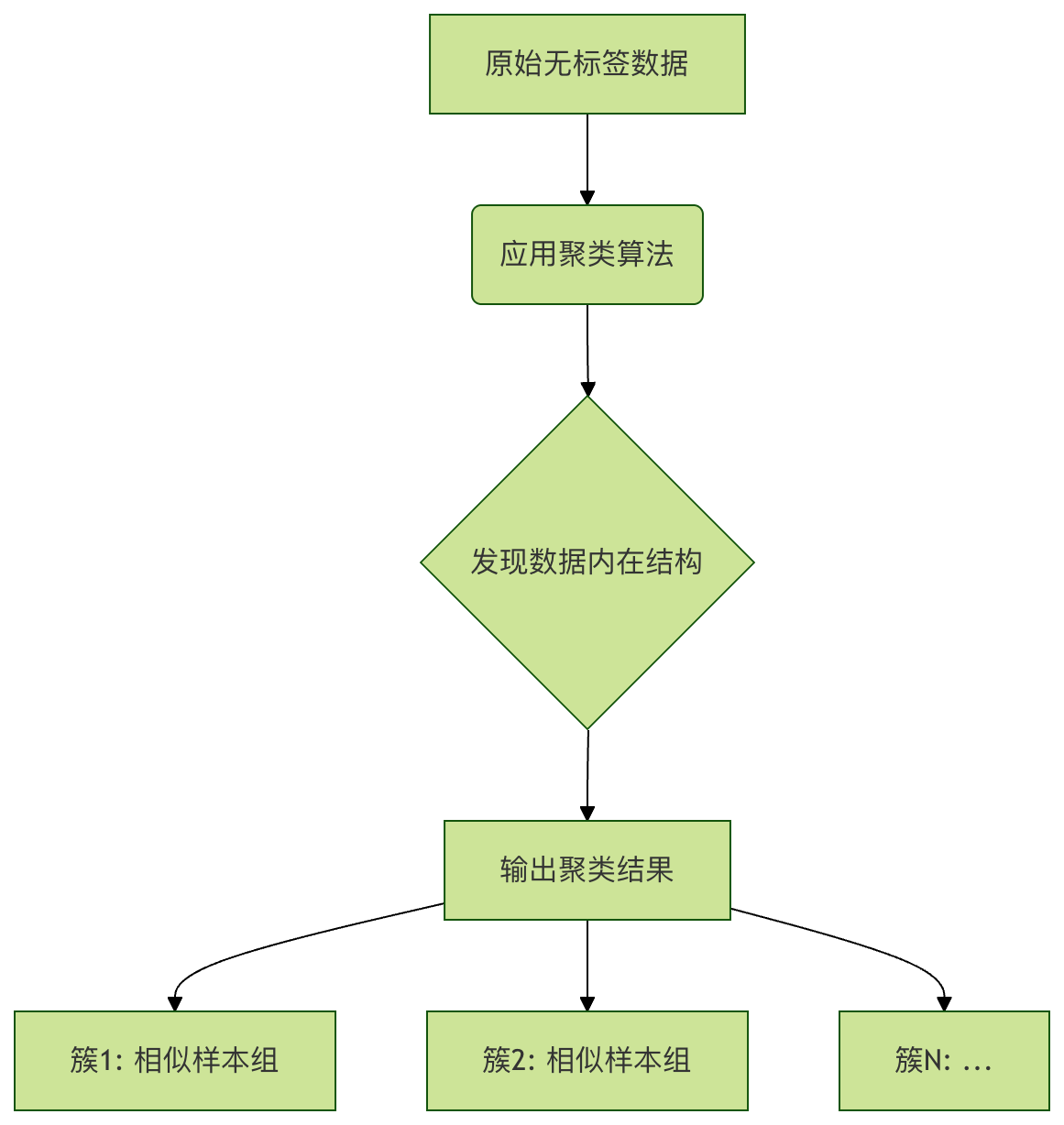
在机器学习中,聚类 要做的正是这样的事情。它是一种无监督学习方法,目标是在没有预先标注答案(即没有"标签")的数据中,发现其内在的结构和分组。
什么是无监督学习与聚类?
在开始之前,我们先快速区分一下机器学习的两大范式:
- 监督学习:就像有老师指导的学习。我们给算法提供大量问题(特征数据)和对应的标准答案(标签),让它学习从问题到答案的映射关系。例如,给算法看很多猫和狗的图片(特征),并告诉它每张图是猫还是狗(标签),训练后它就能识别新的图片。
- 无监督学习:就像让机器自己去探索和发现。我们只提供问题(特征数据),不提供答案(标签)。算法的任务是自行从数据中找出模式、结构或关系。聚类就是其中最核心的技术之一。
聚类的核心思想:将数据集中的样本划分成若干个互不相交的子集(称为簇或类),使得同一个簇内的样本彼此相似,而不同簇中的样本彼此不相似。
这里的相似通常通过数学上的距离来衡量(如欧氏距离)。
距离越近,相似度越高。
经典聚类算法:K-Means
K-Means 是最著名、最常用的聚类算法之一,其思想直观,实现相对简单。
算法原理与步骤
我们可以把 K-Means 的过程想象成竞选代表并重新划区:
- 确定簇的数量 K:首先,你需要决定想把数据分成几类。这个 K 值需要预先指定,这是 K-Means 的一个关键参数。
- 初始化代表(质心):随机在数据空间中选取 K 个点,作为每个簇的初始"中心点",我们称之为质心。
- 分配居民(样本):计算数据集中每一个样本点到这 K 个质心的距离。遵循"近者归其类"的原则,将每个样本分配给距离它最近的那个质心所在的簇。这样,所有样本就被划分到了 K 个簇中。
- 改选新代表更新质心):现在,每个簇里都有了一批样本。重新计算每个簇的质心,新的质心就是该簇内所有样本点的平均值(均值点)。
- 重复与收敛:重复步骤 3(分配)和步骤 4(更新),直到质心的位置不再发生显著变化(即算法收敛)。此时,每个样本的所属簇也不再变化。
代码示例与实践
让我们用 Python 的 scikit-learn 库和一个简单的数据集来演示 K-Means。
实例
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
# -------------------------- 设置中文字体 start --------------------------
plt.rcParams['font.sans-serif'] = [
# Windows 优先
'SimHei', 'Microsoft YaHei',
# macOS 优先
'PingFang SC', 'Heiti TC',
# Linux 优先
'WenQuanYi Micro Hei', 'DejaVu Sans'
]
# 修复负号显示为方块的问题
plt.rcParams['axes.unicode_minus'] = False
# -------------------------- 设置中文字体 end --------------------------
# 1. 创建一个人工数据集
# 我们生成 300 个样本点,它们天然地围绕 4 个中心分布(方便我们观察)
X, y_true = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)
# X 是特征数据,y_true 是真实的类别标签(仅用于最后对比,聚类算法不会用到它)
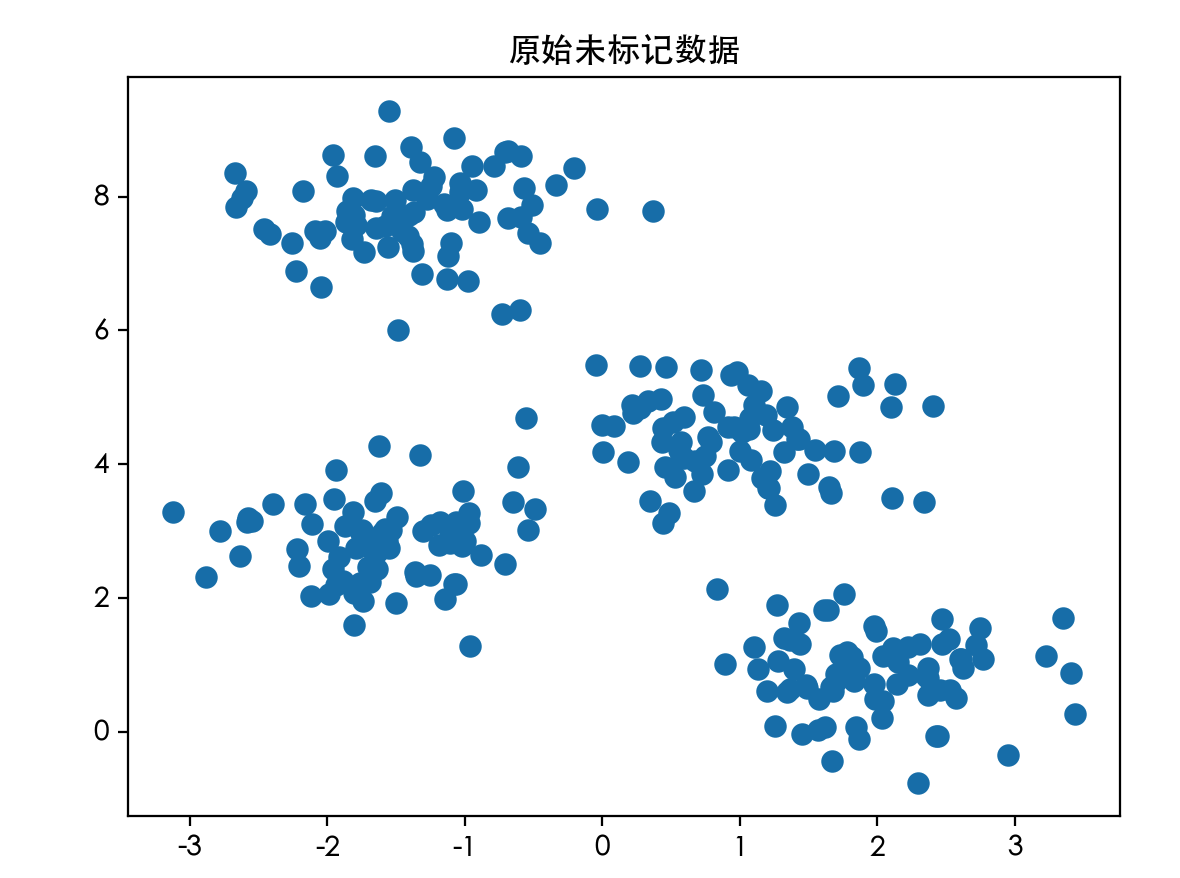
# 2. 可视化原始数据
plt.scatter(X[:, 0], X[:, 1], s=50) # s 是点的大小
plt.title("原始未标记数据")
plt.show()
# 3. 应用 K-Means 聚类
# 指定要聚成 4 类
kmeans = KMeans(n_clusters=4, random_state=0, n_init='auto')
# 拟合模型并预测每个样本的簇标签
y_kmeans = kmeans.fit_predict(X)
# 4. 获取质心坐标
centroids = kmeans.cluster_centers_
# 5. 可视化聚类结果
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')
# 用不同颜色标注不同簇的样本点
plt.scatter(centroids[:, 0], centroids[:, 1], c='red', s=200, alpha=0.8, marker='X')
# 用红色大叉标出质心位置,alpha 是透明度
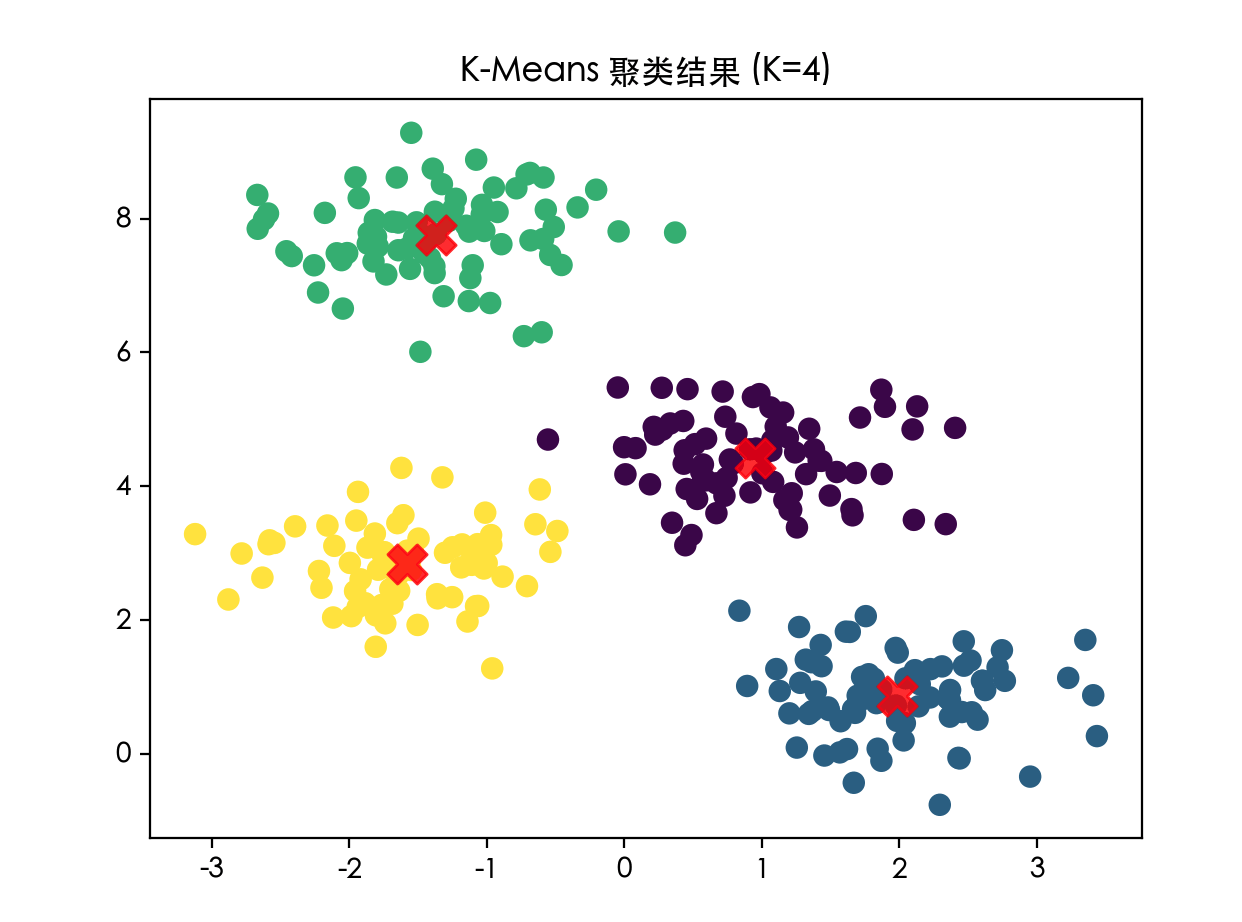
plt.title("K-Means 聚类结果 (K=4)")
plt.show()
# 打印前10个样本的预测簇标签
print("前10个样本的簇标签:", y_kmeans[:10])
# 打印质心坐标
print("四个簇的质心坐标:\n", centroids)
代码解析:
make_blobs:生成用于聚类的模拟数据集,centers=4表示数据围绕 4 个中心点生成。KMeans(n_clusters=4):创建 K-Means 模型实例,指定簇数 K 为 4。n_init='auto'是运行算法的次数,取最佳结果。fit_predict(X):核心方法,在数据X上拟合模型并返回每个样本的簇索引(0, 1, 2, 3)。cluster_centers_:属性,存储训练后得到的 K 个质心的坐标。
运行这段代码,你会看到两张图。第一张是杂乱无章的点,第二张则清晰地分成了四个颜色的组,并且中心有红色的 X 标记。这就是 K-Means 的魔力!
前10个样本的簇标签: [1 2 0 2 1 1 3 0 2 2] 四个簇的质心坐标: [[ 0.94973532 4.41906906] [ 1.98258281 0.86771314] [-1.37324398 7.75368871] [-1.58438467 2.83081263]]
原始未标记数据:
K-Means 聚类结果:
如何选择最佳的 K 值?
在上面的例子中,因为我们知道数据是围绕 4 个中心生成的,所以轻松地设置了 K=4。但在现实世界中,我们往往不知道数据应该分成几类。如何选择 K 呢?
一个常用的方法是 "肘部法则"。其思想是:随着簇数量 K 的增加,样本点到其所属簇质心的平均距离(称为畸变程度或 inertia)会下降。当 K 小于真实簇数时,增加 K 会大幅降低这个距离;当 K 达到真实簇数后,再增加 K,距离的下降幅度会骤减。这个拐点就像手肘的关节,对应的 K 值就是较好的选择。
实例
inertias = []
K_range = range(1, 11) # 测试 K 从 1 到 10
for k in K_range:
kmeans = KMeans(n_clusters=k, random_state=0, n_init='auto')
kmeans.fit(X)
inertias.append(kmeans.inertia_) # inertia_ 属性即 SSE
# 绘制肘部曲线
plt.plot(K_range, inertias, 'bo-')
plt.xlabel('簇的数量 K')
plt.ylabel('Inertia (SSE)')
plt.title('肘部法则寻找最佳 K 值')
plt.axvline(x=4, color='r', linestyle='--', alpha=0.5) # 标记我们已知的 K=4
plt.show()
观察生成的曲线,你会发现在 K=4 附近,曲线下降速度明显变缓,形成一个"肘部",这提示我们 K=4 是一个合理的选择。
聚类的应用场景
聚类是一种强大的探索性数据分析工具,应用极其广泛:
- 客户细分:在电商或营销中,根据客户的购买行为、 demographics(人口统计特征)进行聚类,划分出"高价值客户"、"价格敏感客户"等群体,以便实施精准营销。
- 图像分割:将图像中的像素根据颜色、纹理进行聚类,可以用于简化图像、识别前景和背景。
- 异常检测:正常的数据点通常会形成密集的簇,而异常点则远离任何簇的中心。通过聚类可以发现这些离群点。
- 文档归类:对新闻文章或研究论文进行聚类,自动发现热点话题或研究领域。
- 社交网络分析:在社交网络中,通过对用户的关系、互动进行聚类,可以发现社区或圈子。
实践练习与总结
练习 1:尝试不同的 K 值
修改上面 K-Means 示例代码中的 n_clusters 参数,分别设置为 2, 3, 5, 8。观察聚类结果图,感受 K 值选择对结果的影响。
练习 2:使用真实数据集
尝试使用 scikit-learn 自带的 iris(鸢尾花)数据集进行聚类。虽然这个数据集通常用于分类,但你可以忽略它的标签,只用特征数据(花萼和花瓣的长度宽度)进行 K-Means 聚类,然后将聚类结果与真实标签对比,看看效果如何。
实例
iris = datasets.load_iris()
X_iris = iris.data # 只使用特征数据

点我分享笔记