TensorFlow 核心概念

TensorFlow 的名字来源于其处理数据的核心结构 - 张量（Tensor）和计算流程（Flow）。

TensorFlow 是一个端到端的开源机器学习平台，它的核心优势在于：

  • 灵活的计算图模型：支持动态图和静态图两种模式
  • 跨平台部署能力：可在 CPU、GPU、TPU 和移动设备上运行
  • 丰富的生态系统：包含 TensorFlow Lite（移动端）、TensorFlow.js（浏览器端）等子项目
  • 生产就绪：提供从研究到生产的完整工具链

核心概念解析

张量（Tensor）

张量是 TensorFlow 中最基本的数据结构，可以理解为多维数组的泛化概念。

从数学角度来说，张量是一个可以用来表示在一些矢量、标量和其他张量之间的线性关系的多线性函数。

简单类比：

  • 标量（0维张量）：一个数字，如 5
  • 向量（1维张量）：一列数字，如 [1, 2, 3, 4]
  • 矩阵（2维张量）：数字的表格，如 [[1, 2], [3, 4]]
  • 3维张量：数字的立方体，如彩色图像（高×宽×颜色通道）
  • 更高维张量：例如视频数据（时间×高×宽×颜色通道）

张量的关键属性

实例

# 示例张量
import tensorflow as tf

# 创建一个 2x3 的矩阵张量
tensor = tf.constant([[1, 2, 3], [4, 5, 6]])

print(f"形状 (Shape): {tensor.shape}")        # (2, 3)
print(f"数据类型 (Dtype): {tensor.dtype}")    # int32
print(f"维度 (Rank): {tf.rank(tensor)}")      # 2
print(f"设备 (Device): {tensor.device}")      # /job:localhost/replica:0/task:0/device:CPU:0

关键属性解释：

  1. 形状（Shape）：描述每个维度的大小

    • (2, 3) 表示 2 行 3 列的矩阵
    • (224, 224, 3) 表示 224×224 像素的 RGB 图像

  2. 数据类型（Dtype）：张量中数据的类型

    • tf.float32：32位浮点数（最常用）
    • tf.int32：32位整数
    • tf.bool：布尔值
    • tf.string：字符串

  3. 维度/秩（Rank）：张量的维数

    • 标量：秩为 0
    • 向量：秩为 1
    • 矩阵：秩为 2

  4. 设备（Device）：张量存储的设备位置

    • CPU：/device:CPU:0
    • GPU：/device:GPU:0

张量在机器学习中的意义

数据表示：

  • 输入数据：图像、文本、音频都可以表示为张量
  • 模型参数：权重和偏置都是张量
  • 中间结果：计算过程中的所有数据都是张量
  • 输出结果：预测结果、损失值等

实际例子：

  • 图像分类：输入张量形状 (batch_size, height, width, channels)
  • 文本处理：输入张量形状 (batch_size, sequence_length)
  • 时间序列：输入张量形状 (batch_size, time_steps, features)

计算图（Computational Graph）

计算图是一种用节点和边来表示数学运算的图结构：

  • 节点（Node）：代表数学运算（加法、乘法、激活函数等）
  • 边（Edge）：代表数据流动的路径（张量）

简单例子：

计算 z = (x + y) * w 的计算图：

x ──┐
    ├─→ [+] ──→ [×] ──→ z
y ──┘         ├
w ────────────┘

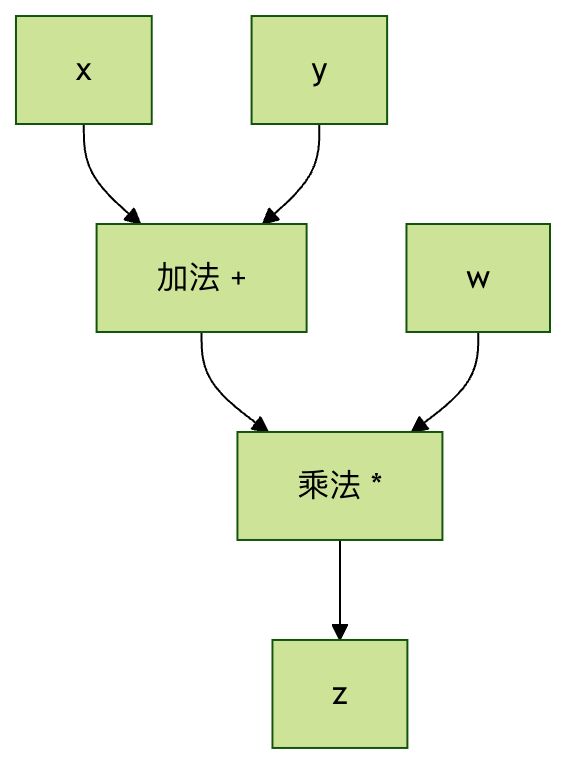
计算图的优势

1. 自动微分：

  • 可以自动计算梯度，实现反向传播
  • 不需要手动推导复杂的梯度公式

2. 优化机会：

  • 编译时优化：合并运算、消除冗余
  • 运行时优化：内存复用、并行计算

3. 可视化调试：

  • 使用 TensorBoard 可视化模型结构
  • 便于理解和调试复杂模型

4. 分布式计算：

  • 可以将图的不同部分分配到不同设备
  • 支持跨机器的分布式训练

静态图 vs 动态图

TensorFlow 1.x（静态图）：

实例

# TensorFlow 1.x 风格（仅作理解，不推荐使用）
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()

# 定义计算图
x = tf.placeholder(tf.float32, shape=[None, 784])
W = tf.Variable(tf.random.normal([784, 10]))
b = tf.Variable(tf.zeros([10]))
y = tf.matmul(x, W) + b

# 创建会话并执行
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    result = sess.run(y, feed_dict={x: input_data})

TensorFlow 2.x（动态图/即时执行）：

实例

# TensorFlow 2.x 风格（推荐）
import tensorflow as tf

# 直接执行运算
x = tf.constant([[1.0, 2.0, 3.0]])
W = tf.Variable(tf.random.normal([3, 2]))
b = tf.Variable(tf.zeros([2]))
y = tf.matmul(x, W) + b

print(y)  # 立即得到结果

会话（Session）与即时执行（Eager Execution）

TensorFlow 1.x 的会话机制

在 TensorFlow 1.x 中，计算图的构建和执行是分离的：

两阶段过程：

  1. 构建阶段：定义计算图，但不执行任何计算
  2. 执行阶段：在会话中运行图，获得结果

会话的作用：

  • 管理图的执行环境
  • 分配和管理资源（内存、设备）
  • 提供图执行的上下文

3.2 TensorFlow 2.x 的即时执行

TensorFlow 2.x 默认启用即时执行，让 TensorFlow 变得更加 "Pythonic"：

即时执行的特点：

  • 立即求值：运算定义后立即执行
  • 易于调试：可以使用 Python 调试工具
  • 直观编程：像写普通 Python 代码一样

对比示例：

实例

# TensorFlow 2.x - 即时执行
import tensorflow as tf

a = tf.constant(2.0)
b = tf.constant(3.0)
c = a + b
print(f"结果: {c}")  # 结果: 5.0

# 可以直接访问值
print(f"c 的 numpy 值: {c.numpy()}")  # c 的 numpy 值: 5.0

图模式 vs 即时执行模式

即时执行模式（默认，适合开发调试）：

  • 运算立即执行
  • 易于调试和理解
  • 性能略低

图模式（适合生产部署）：

  • 预先构建完整计算图
  • 更好的优化机会
  • 更高的执行效率

切换到图模式：

实例

@tf.function
def compute_function(x, y):
    return x * y + x

# 这个函数会被编译成图
result = compute_function(tf.constant(2.0), tf.constant(3.0))

变量（Variable）和常量（Constant）

常量（Constant）

常量是不可变的张量，一旦创建就不能修改：

实例

# 创建常量
scalar_const = tf.constant(3.14)
vector_const = tf.constant([1, 2, 3, 4])
matrix_const = tf.constant([[1, 2], [3, 4]])

# 常量的值不能改变
print(scalar_const)  # tf.Tensor(3.14, shape=(), dtype=float32)

常量的用途：

  • 存储超参数（学习率、批大小等）
  • 存储不需要训练的配置数据
  • 作为计算中的固定值

变量（Variable）

变量是可变的张量，通常用来存储模型参数：

实例

# 创建变量
weight = tf.Variable(tf.random.normal([2, 3]))
bias = tf.Variable(tf.zeros([3]))

print(f"初始权重:\n{weight}")

# 修改变量的值
weight.assign(tf.ones([2, 3]))
print(f"修改后权重:\n{weight}")

# 部分更新
weight[0, 0].assign(5.0)
print(f"部分更新后:\n{weight}")

变量的关键特性：

  1. 状态保持：在训练过程中保持状态
  2. 梯度跟踪：可以计算相对于变量的梯度
  3. 可优化：可以被优化算法更新
  4. 可保存：可以保存到检查点文件

变量 vs 常量的使用场景

特性 变量（Variable） 常量（Constant）
可变性 可修改 不可修改
主要用途 模型参数（权重、偏置） 超参数、输入数据
梯度计算 支持 不支持
内存占用 持久存储 临时存储
典型例子 W = tf.Variable(...) learning_rate = tf.constant(0.01)

数据流动和自动微分

前向传播

数据在计算图中从输入节点流向输出节点的过程：

实例

# 简单的前向传播示例
import tensorflow as tf

# 输入数据
x = tf.constant([[1.0, 2.0]])

# 模型参数
W1 = tf.Variable(tf.random.normal([2, 3]))
b1 = tf.Variable(tf.zeros([3]))
W2 = tf.Variable(tf.random.normal([3, 1]))
b2 = tf.Variable(tf.zeros([1]))

# 前向传播
hidden = tf.nn.relu(tf.matmul(x, W1) + b1)  # 隐层
output = tf.matmul(hidden, W2) + b2         # 输出层

print(f"最终输出: {output}")

自动微分（Automatic Differentiation）

TensorFlow 使用 GradientTape 来记录运算并自动计算梯度：

实例

# 自动微分示例
x = tf.Variable(3.0)

# 使用 GradientTape 记录运算
with tf.GradientTape() as tape:
    y = x**2 + 2*x + 1  # y = x² + 2x + 1

# 计算 dy/dx
gradient = tape.gradient(y, x)
print(f"当 x=3 时，dy/dx = {gradient}")  # 应该是 2x + 2 = 8

GradientTape 的工作原理：

  1. 记录运算：tape 记录所有在其上下文中的运算
  2. 构建反向图：创建用于梯度计算的反向计算图
  3. 计算梯度：使用链式法则计算梯度

训练循环中的概念整合

实例

# 完整的训练步骤示例
import tensorflow as tf

# 模型和数据
model = tf.keras.Sequential([
    tf.keras.layers.Dense(10, activation='relu'),
    tf.keras.layers.Dense(1)
])

x_train = tf.random.normal([100, 5])
y_train = tf.random.normal([100, 1])

optimizer = tf.keras.optimizers.Adam(0.01)

# 训练步骤
@tf.function
def train_step(x, y):
    with tf.GradientTape() as tape:
        predictions = model(x)
        loss = tf.keras.losses.mse(y, predictions)
   
    gradients = tape.gradient(loss, model.trainable_variables)
    optimizer.apply_gradients(zip(gradients, model.trainable_variables))
    return loss

# 执行训练
for epoch in range(10):
    loss = train_step(x_train, y_train)
    print(f"Epoch {epoch}: Loss = {loss:.4f}")

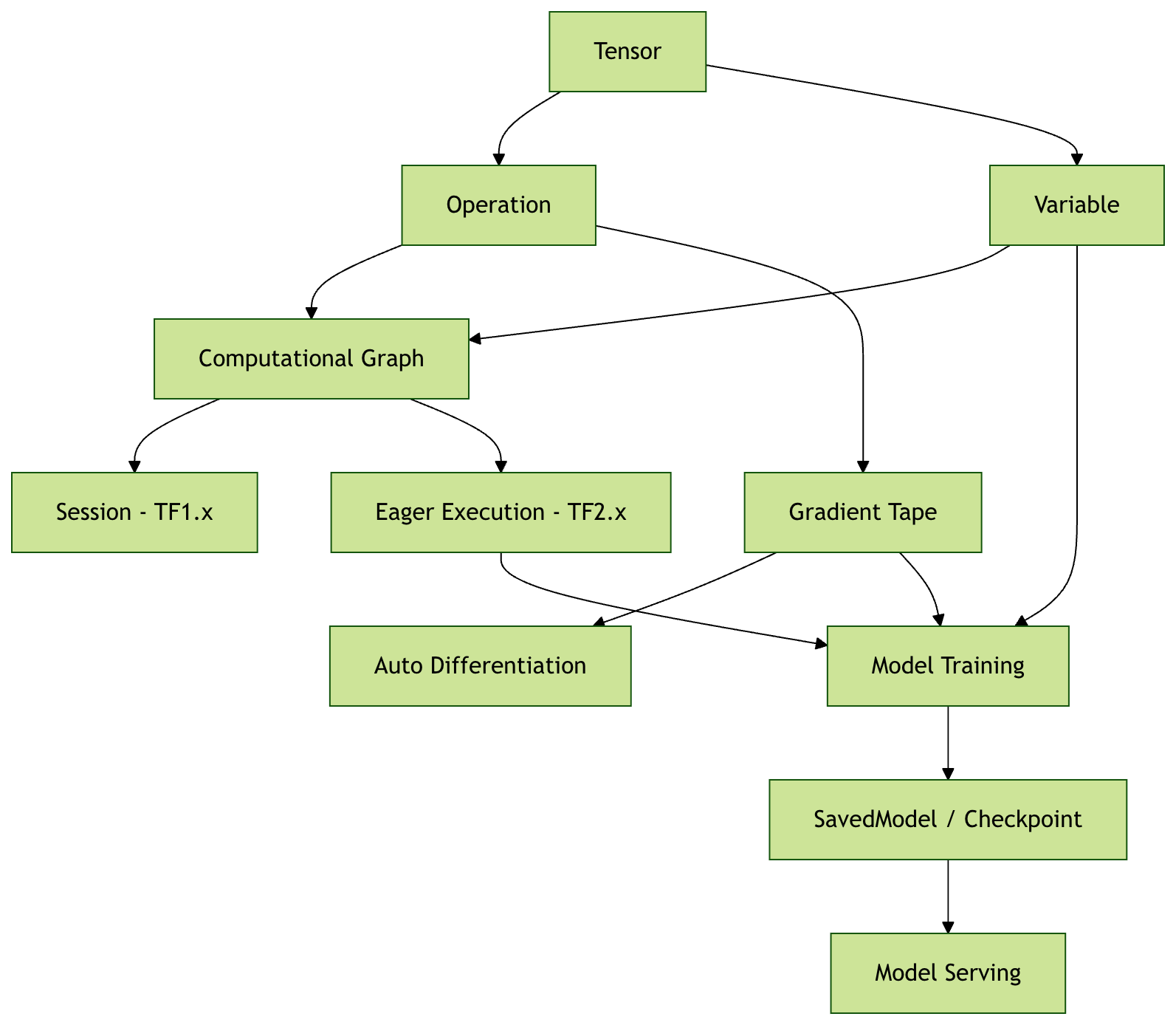
核心概念总结

概念关系图

TensorFlow 核心概念关系：

输入数据 (Tensor) ──→ 计算图 (Graph) ──→ 输出结果 (Tensor)
      ↑                    ↓
   常量/变量            前向传播
      ↑                    ↓
   参数存储 ←──── 梯度更新 ←──── 自动微分
                              ↑
                        GradientTape