排序算法

排序算法（英语：Sorting algorithm）是一种能将一串资料依照特定排序方式排列的算法，排序后的资料即可放在有序数组。

排序 是指将一组数据（例如一个数组或列表）按照某种特定的顺序（升序或降序）重新排列的过程。

排序的依据通常是数据元素的某个关键码，比如数字的大小、字符串的字典序等。

排序是计算机科学中最基础、最核心的算法问题之一。无论是整理通讯录、分析考试成绩，还是数据库查询优化，排序算法都无处不在。理解不同的排序算法，不仅能帮助我们解决实际问题，更是深入理解算法设计与分析思想的绝佳途径。

排序算法的分类

排序算法可以从多个维度进行分类，最常见的分类方式是基于其时间复杂度和空间复杂度。

分类维度 类别 说明 典型算法
时间复杂度 O(n²) 级 简单直观，但效率较低，适合小规模数据。 冒泡排序、选择排序、插入排序
O(n log n) 级 效率较高，是处理大规模数据的首选。 快速排序、归并排序、堆排序
空间复杂度 原地排序 排序过程中只使用常数级别的额外空间。 冒泡、选择、插入、希尔、堆排序、快速排序
非原地排序 排序过程中需要借助与数据规模相当的额外空间。 归并排序、计数排序、桶排序、基数排序
稳定性 稳定排序 相等元素的相对顺序在排序后保持不变。 冒泡、插入、归并、计数、桶、基数排序
不稳定排序 相等元素的相对顺序在排序后可能改变。 选择、希尔、堆、快速排序

关键概念解释：

  • 时间复杂度：衡量算法执行时间随数据量增长的趋势。
  • 空间复杂度：衡量算法执行过程中所需额外存储空间的大小。
  • 稳定性：对于值相等的元素，排序后它们的前后关系是否保持不变。这在多关键字排序时非常重要。

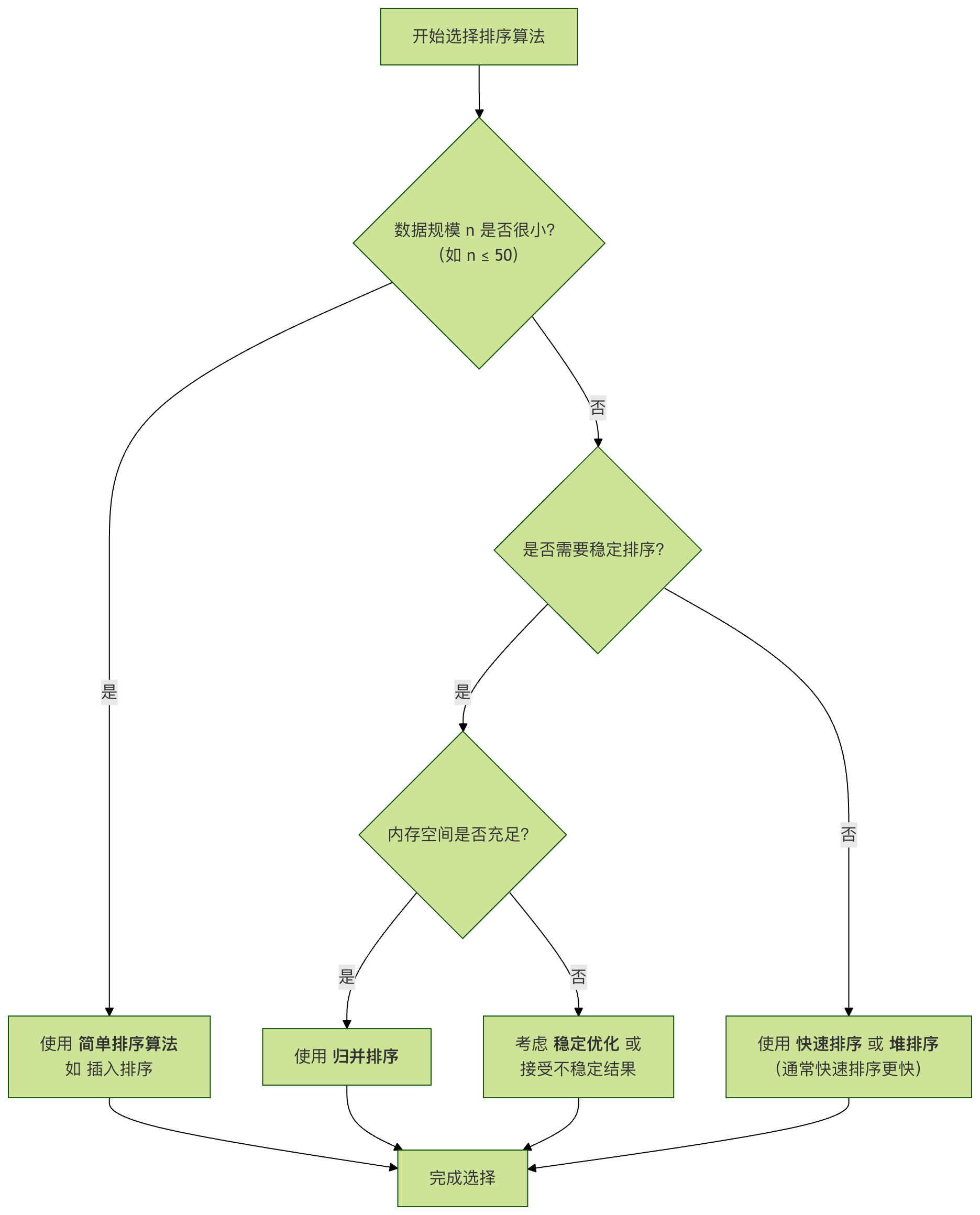
下面的流程图展示了如何根据不同的需求场景，在几种经典算法中做出初步选择：

O(n²) 级基础排序算法

这类算法思想简单，是理解排序逻辑的起点。

冒泡排序

核心思想：重复"遍历"待排序序列，一次比较两个相邻元素，如果它们的顺序错误就把它们交换过来。每一轮遍历都会将当前未排序部分的最大（或最小）元素冒泡到正确位置。

算法步骤：

  1. 比较相邻的元素。如果第一个比第二个大（升序），就交换它们两个。
  2. 对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
  3. 针对所有的元素重复以上的步骤，除了最后一个（因为每一轮都会确定一个最终元素）。
  4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

代码实现：

实例

def bubble_sort(arr):
    """
    冒泡排序 (升序)
    :param arr: 待排序的列表
    """
    n = len(arr)
    # 外层循环控制需要进行的轮数 (n-1 轮)
    for i in range(n - 1):
        # 内层循环进行相邻元素的比较和交换
        # 每轮结束后，最后 i+1 个元素已有序，所以比较范围是 0 到 n-1-i
        for j in range(0, n - 1 - i):
            if arr[j] > arr[j + 1]:  # 如果前面的元素比后面大
                # 交换两个元素的位置
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
    return arr

# 测试数据
test_data = [64, 34, 25, 12, 22, 11, 90]
print("原始数组:", test_data)
sorted_data = bubble_sort(test_data.copy()) # 使用副本，避免修改原数据
print("冒泡排序后:", sorted_data)

输出：

原始数组: [64, 34, 25, 12, 22, 11, 90]
冒泡排序后: [11, 12, 22, 25, 34, 64, 90]

性能分析：

  • 时间复杂度：最好情况 O(n)（已有序时，可通过优化实现），最坏和平均情况 O(n²)。
  • 空间复杂度：O(1)，是原地排序。
  • 稳定性：稳定。

选择排序

核心思想：在未排序序列中找到最小（或最大）元素，存放到排序序列的起始位置，然后再从剩余未排序元素中继续寻找最小（大）元素，放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

算法步骤：

  1. 初始状态：整个序列为无序区。
  2. 第 i 轮（i 从 0 开始）排序时，当前无序区为 arr[i...n-1]。从该区中选出关键字最小的记录 arr[min_index]。
  3. 将 arr[min_index] 与无序区的第一个记录 arr[i] 交换。这样，arr[0...i] 就形成了有序区。
  4. n-1 轮结束后，数组排序完成。

代码实现：

实例

def selection_sort(arr):
    """
    选择排序 (升序)
    :param arr: 待排序的列表
    """
    n = len(arr)
    for i in range(n):
        # 假设当前索引 i 的元素是最小的
        min_index = i
        # 在 i+1 到 n-1 的范围内寻找更小的元素
        for j in range(i + 1, n):
            if arr[j] < arr[min_index]:
                min_index = j # 更新最小元素的索引
        # 将找到的最小元素与位置 i 的元素交换
        arr[i], arr[min_index] = arr[min_index], arr[i]
    return arr

# 测试
test_data = [64, 25, 12, 22, 11]
print("原始数组:", test_data)
print("选择排序后:", selection_sort(test_data.copy()))

输出：

原始数组: [64, 25, 12, 22, 11]
选择排序后: [11, 12, 22, 25, 64]

性能分析：

  • 时间复杂度：始终为 O(n²)，因为无论数据是否有序，都需要进行完整的比较。
  • 空间复杂度：O(1)，原地排序。
  • 稳定性：不稳定。例如序列 [5, 8, 5, 2, 9]，第一轮会将第一个 5 和 2 交换，破坏了两个 5 原有的顺序。

插入排序

核心思想：通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。这就像我们整理扑克牌一样。

算法步骤：

  1. 将第一个元素视为已排序序列。
  2. 取出下一个元素，在已经排序的元素序列中从后向前扫描。
  3. 如果该元素（已排序）大于新元素，将该元素移到下一位置。
  4. 重复步骤 3，直到找到已排序的元素小于或等于新元素的位置。
  5. 将新元素插入到该位置后。
  6. 重复步骤 2~5，直到所有元素处理完毕。

代码实现：

实例

def insertion_sort(arr):
    """
    插入排序 (升序)
    :param arr: 待排序的列表
    """
    n = len(arr)
    # 从第二个元素开始（索引1），因为第一个元素默认已排序
    for i in range(1, n):
        key = arr[i]  # 当前待插入的元素
        j = i - 1     # 已排序序列的最后一个元素的索引
        # 从后向前扫描已排序序列，寻找 key 的插入位置
        # 同时将大于 key 的元素向后移动一位
        while j >= 0 and key < arr[j]:
            arr[j + 1] = arr[j]
            j -= 1
        # 将 key 插入到找到的正确位置
        arr[j + 1] = key
    return arr

# 测试
test_data = [12, 11, 13, 5, 6]
print("原始数组:", test_data)
print("插入排序后:", insertion_sort(test_data.copy()))

输出：

原始数组: [12, 11, 13, 5, 6]
插入排序后: [5, 6, 11, 12, 13]

性能分析：

  • 时间复杂度：最好情况 O(n)（已有序），最坏和平均情况 O(n²)。
  • 空间复杂度：O(1)，原地排序。
  • 稳定性：稳定。
  • 特点：对于小规模或基本有序的数据，插入排序非常高效。它是高级排序算法（如 Timsort）在小规模数据时切换使用的算法。

O(n log n) 级高效排序算法

当数据量变大时，O(n²) 的算法会变得非常慢。下面这些更高效的算法是工程实践中的主力。

快速排序

核心思想：分治法。选择一个基准元素，通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，然后分别对这两部分记录继续进行排序，以达到整个序列有序。

算法步骤：

  1. 选择基准：从数列中挑出一个元素，称为"基准"。
  2. 分区操作：重新排列数列，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区操作。
  3. 递归排序：递归地将小于基准值元素的子数列和大于基准值元素的子数列排序。

代码实现：

实例

def quick_sort(arr):
    """
    快速排序 (升序) - 主函数
    """
    def _quick_sort(arr, low, high):
        if low < high:
            # pi 是分区索引，arr[pi] 现在在正确位置
            pi = partition(arr, low, high)
            # 递归排序分区前后的子数组
            _quick_sort(arr, low, pi - 1)
            _quick_sort(arr, pi + 1, high)

    def partition(arr, low, high):
        """
        分区函数，选择最后一个元素作为基准(pivot)
        :return: 基准元素的最终正确位置索引
        """
        pivot = arr[high]  # 选择基准
        i = low - 1        # 指向小于基准的子数组的末尾
        for j in range(low, high):
            # 如果当前元素小于或等于基准
            if arr[j] <= pivot:
                i += 1
                arr[i], arr[j] = arr[j], arr[i] # 交换
        # 将基准元素放到正确的位置（i+1）
        arr[i + 1], arr[high] = arr[high], arr[i + 1]
        return i + 1

    _quick_sort(arr, 0, len(arr) - 1)
    return arr

# 测试
test_data = [10, 80, 30, 90, 40, 50, 70]
print("原始数组:", test_data)
print("快速排序后:", quick_sort(test_data.copy()))

输出：

原始数组: [10, 80, 30, 90, 40, 50, 70]
快速排序后: [10, 30, 40, 50, 70, 80, 90]

性能分析：

  • 时间复杂度：平均情况 O(n log n)，最坏情况 O(n²)（当数组已有序或逆序，且基准选择不当时）。通过随机选择基准或"三数取中"法可以极大避免最坏情况。
  • 空间复杂度：平均 O(log n)（递归调用栈），最坏 O(n)。
  • 稳定性：不稳定。

归并排序

核心思想：分治法的典型应用。将已有序的子序列合并，得到完全有序的序列。即先使每个子序列有序，再使子序列段间有序。

算法步骤：

  1. 分解：将当前区间一分为二，即求分裂点 mid = (low + high)/2。
  2. 求解：递归地对两个子区间 arr[low...mid] 和 arr[mid+1...high] 进行归并排序。递归的终止条件是子区间长度为1（认为一个元素自然有序）。
  3. 合并：将两个已排序的子区间合并为一个有序区间。

代码实现：

实例

def merge_sort(arr):
    """
    归并排序 (升序) - 主函数
    """
    if len(arr) > 1:
        mid = len(arr) // 2  # 找到中间点，分割数组
        left_half = arr[:mid]
        right_half = arr[mid:]

        # 递归调用对左右两半进行排序
        merge_sort(left_half)
        merge_sort(right_half)

        # 合并两个已排序的子数组
        i = j = k = 0
        # 比较左右子数组的元素，将较小的放入原数组
        while i < len(left_half) and j < len(right_half):
            if left_half[i] < right_half[j]:
                arr[k] = left_half[i]
                i += 1
            else:
                arr[k] = right_half[j]
                j += 1
            k += 1

        # 检查是否有剩余元素（左半部分或右半部分）
        while i < len(left_half):
            arr[k] = left_half[i]
            i += 1
            k += 1
        while j < len(right_half):
            arr[k] = right_half[j]
            j += 1
            k += 1
    return arr

# 测试
test_data = [38, 27, 43, 3, 9, 82, 10]
print("原始数组:", test_data)
print("归并排序后:", merge_sort(test_data.copy()))

输出：

原始数组: [38, 27, 43, 3, 9, 82, 10]
归并排序后: [3, 9, 10, 27, 38, 43, 82]

性能分析：

  • 时间复杂度：最好、最坏、平均情况均为 O(n log n)。性能非常稳定。
  • 空间复杂度：O(n)，需要与原始数组等大的额外空间来合并。
  • 稳定性：稳定。

堆排序

核心思想：利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆的性质：即父节点的值总是大于或等于（最大堆）或小于或等于（最小堆）任何子节点的值。

算法步骤：

  1. 构建最大堆：将待排序序列构造成一个最大堆。此时，整个序列的最大值就是堆顶的根节点。
  2. 交换堆顶与末尾元素：将堆顶元素（最大值）与末尾元素交换，此时末尾元素为最大值。
  3. 调整堆结构：将剩余 n-1 个元素重新构造成一个最大堆，这样会得到次大值。将其与新末尾（n-1位置）交换。
  4. 重复执行 步骤 2 和 3，直到堆的大小为 1，排序完成。

代码实现：

实例

def heap_sort(arr):
    """
    堆排序 (升序) - 使用最大堆
    """
    n = len(arr)

    # 步骤1：构建最大堆。从最后一个非叶子节点开始向上调整
    # 最后一个非叶子节点的索引 = n//2 - 1
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)

    # 步骤2 & 3：逐个提取堆顶元素（最大值）并调整堆
    for i in range(n - 1, 0, -1):
        # 将当前堆顶（最大值）与末尾元素交换
        arr[i], arr[0] = arr[0], arr[i]
        # 调整剩余元素，使其重新成为最大堆，堆大小变为 i
        heapify(arr, i, 0)
    return arr

def heapify(arr, n, i):
    """
    调整以 i 为根的子树，使其成为最大堆
    :param arr: 堆数组
    :param n: 堆的当前大小
    :param i: 当前根节点的索引
    """
    largest = i         # 初始化最大值为根
    left = 2 * i + 1    # 左子节点索引
    right = 2 * i + 2   # 右子节点索引

    # 如果左子节点存在且大于根
    if left < n and arr[left] > arr[largest]:
        largest = left
    # 如果右子节点存在且大于当前最大值
    if right < n and arr[right] > arr[largest]:
        largest = right
    # 如果最大值不是根，则交换并递归调整被破坏的子堆
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)

# 测试
test_data = [4, 10, 3, 5, 1]
print("原始数组:", test_data)
print("堆排序后:", heap_sort(test_data.copy()))

输出：

原始数组: [4, 10, 3, 5, 1]
堆排序后: [1, 3, 4, 5, 10]

性能分析：

  • 时间复杂度：最好、最坏、平均情况均为 O(n log n)。
  • 空间复杂度：O(1)，原地排序。
  • 稳定性：不稳定。

算法性能对比总结

为了更直观地比较上述算法的特性，我们将其汇总如下表：

算法 平均时间复杂度 最坏时间复杂度 空间复杂度 稳定性 主要特点
冒泡排序 O(n²) O(n²) O(1) 稳定 简单，效率低，适合教学。
选择排序 O(n²) O(n²) O(1) 不稳定 交换次数少，但比较次数固定多。
插入排序 O(n²) O(n²) O(1) 稳定 对小规模或基本有序数据高效。
快速排序 O(n log n) O(n²) O(log n) 不稳定 平均性能最好，是应用最广的排序算法。
归并排序 O(n log n) O(n log n) O(n) 稳定 性能稳定，但需要额外空间。常用于外部排序。
堆排序 O(n log n) O(n log n) O(1) 不稳定 原地排序且最坏情况也是 O(n log n)。

实践练习

理论学习之后，动手实践是巩固知识的最佳方式。

练习 1：算法选择与实现

给定以下场景，你会选择哪种排序算法？并简要说明理由。

  1. 对一个包含 10 个数字的数组进行排序。
  2. 对一个包含 100 万个学生对象的链表按学号排序，要求稳定。
  3. 在一个内存有限的嵌入式系统中，对一个大型数组进行排序。
  4. 需要实时获取数据流中前 K 个最大元素。

参考答案思路：

  1. 插入排序。数据规模小，插入排序简单且对近乎有序数据友好，常数因子小。
  2. 归并排序。数据规模大，要求稳定排序，且链表结构使得归并排序的合并操作可以在 O(1) 空间内完成（修改指针即可）。
  3. 堆排序。内存有限，需要原地排序，且堆排序在最坏情况下也能保证 O(n log n) 的性能。
  4. 维护一个大小为 K 的最小堆。遍历数据流，用堆来维护当前最大的 K 个元素。这不是完整的排序，但利用了堆的特性。

练习 2：代码调试与优化

下面的冒泡排序有一个小 bug 和一处可优化的地方，请找出并修复。

实例

def bubble_sort_buggy(arr):
    n = len(arr)
    for i in range(n):
        for j in range(n - 1):
            if arr[j] > arr[j]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
    return arr

提示：

  • 比较条件 arr[j] > arr[j] 永远为假。
  • 内层循环的边界可以优化，因为每轮过后，末尾的元素已经有序。

练习 3：动手实现

尝试自己从头实现快速排序，并思考：

  • 如果基准 pivot 总是选择第一个元素，对已排序的数组排序会怎样？
  • 如何修改 partition 函数，使其变为"三路快排"，能更高效地处理大量重复元素的数组？