图论结构

在计算机科学中，图被广泛用于模拟社交网络（用户是点，好友关系是线）、网页链接（网页是点，超链接是线）、通信网络乃至路径规划等问题。

图就像是一张社交网络关系图：

  • 节点（顶点）：社交网络中的每个人
  • 边：人与人之间的关系（好友、关注等）
  • 权重：关系的强度（亲密度、互动频率等）

想象一下你所在城市的交通网络：各个地点（如家、学校、商场）是点，连接这些地点的道路是线。图（Graph）就是这种点和线关系的数学抽象，它是用于表示实体间复杂关系的一种数据结构。

现实生活中的案例：

  • 地图：城市是节点，道路是边，距离是权重
  • 电路：元件是节点，导线是边，电阻是权重
  • 互联网：网站是节点，链接是边，流量是权重
  • 交通网络：车站是节点，线路是边，票价是权重
场景 其他结构 图结构
社交关系 难以表达复杂关系 自然表达多对多关系
路径规划 需要复杂的数据结构 直观表示网络和路径
依赖关系 难以表示循环依赖 轻松处理复杂依赖
网络分析 无法表达网络拓扑 完美描述网络结构

图的基本术语

术语 定义 生活比喻 符号表示
顶点（Vertex） 图中的基本单元 社交网络中的人 V, u, v
边（Edge） 连接两个顶点的线 两人之间的关系 E, (u,v)
度（Degree） 顶点连接的边数 一个人的好友数量 deg(v)
路径（Path） 顶点的序列 从A到B的路线 v₁→v₂→…→vₙ
环（Cycle） 起点和终点相同的路径 从家出发最终回家 v₁→v₂→…→v₁
连通图 任意两点间都有路径 所有人都能互相联系
权重（Weight） 边的数值属性 两城市间的距离 w(u,v)

图的分类

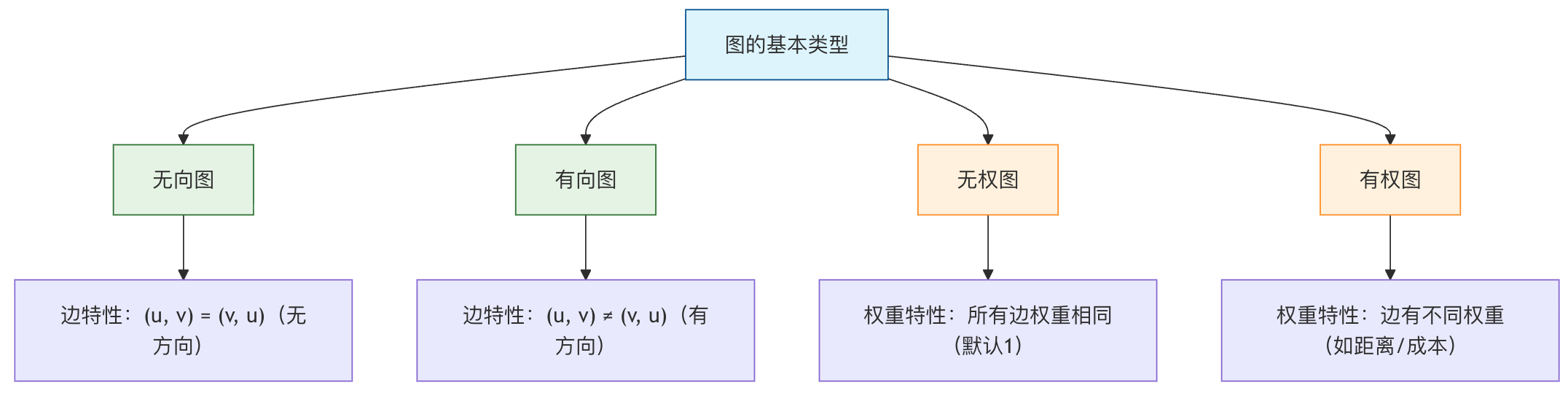
分类标准 类型 特点 应用场景
方向性 无向图 边没有方向 好友关系、道路网络
有向图 边有方向 关注关系、工作流程
权重 无权图 所有边权重相同 社交网络关系
有权图 边有不同权重 地图距离、网络流量
连通性 连通图 任意两点可达 交通网络
非连通图 存在孤立点 社交群体
环 无环图 没有环路 任务依赖、家族树
有环图 包含环路 道路网络

图的表示方法

邻接矩阵

特性 描述 时间复杂度 空间复杂度
存储方式 二维矩阵
检查边存在 matrix[i][j] != 0 O(1)
添加边 matrix[i][j] = weight O(1)
删除边 matrix[i][j] = 0 O(1)
遍历邻接点 扫描一行/列 O(V)
空间占用 V×V矩阵 O(V²)

邻接表

特性 描述 时间复杂度 空间复杂度
存储方式 数组+链表
检查边存在 在链表中查找 O(deg(v))
添加边 在链表中添加 O(1)
删除边 在链表中删除 O(deg(v))
遍历邻接点 遍历链表 O(deg(v))
空间占用 顶点数组+边链表 O(V+E)

图的基本概念

一个图 G 由两个集合构成：

  • 顶点集 V (Vertex Set): 图中所有点的集合。
  • 边集 E (Edge Set): 连接这些点的线的集合。一条边由其连接的两个顶点 (u, v) 表示。

实例

# 一个简单的图示例：用字典表示社交网络好友关系
# 顶点： Alice, Bob, Charlie, Diana
# 边： 表示他们之间的好友关系

social_graph = {
    'Alice': ['Bob', 'Charlie'],   # Alice 是 Bob 和 Charlie 的好友
    'Bob': ['Alice', 'Charlie', 'Diana'],
    'Charlie': ['Alice', 'Bob'],
    'Diana': ['Bob']
}

print(f"顶点（用户）: {list(social_graph.keys())}")
print(f"Alice 的好友（边）: {social_graph['Alice']}")

输出：

顶点（用户）: ['Alice', 'Bob', 'Charlie', 'Diana']
Alice 的好友（边）: ['Bob', 'Charlie']

图的分类与重要概念

图可以根据其边的特性分为多种类型，理解这些是掌握图论的基础。

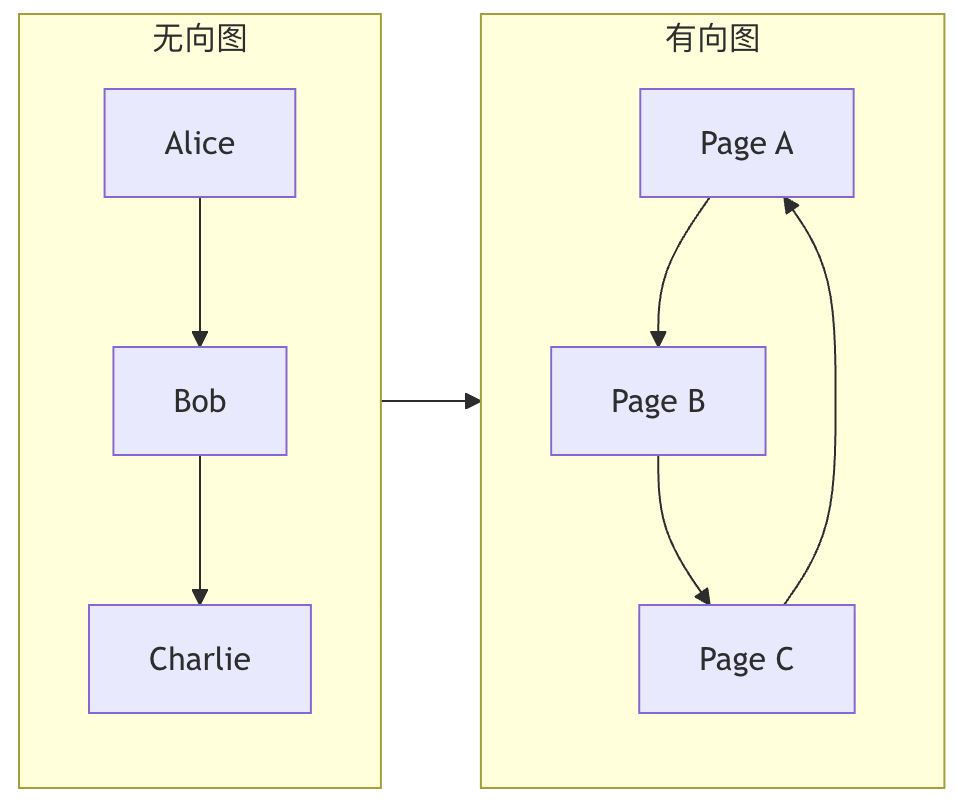
无向图 vs 有向图

类型 边（Edge）的特点 生活类比 示例
无向图 边没有方向，(A, B) 表示 A 和 B 互相连接。 双向友谊：如果 Alice 是 Bob 的朋友，那么 Bob 也一定是 Alice 的朋友。 社交网络中的好友关系、电路中的连接。
有向图 边有方向，A -> B 表示从 A 指向 B 的单向连接。 微博关注：你可以关注某人，但对方不一定关注你。 网页超链接、任务依赖关系、交通单行道。

权重图

在权重图中，每条边都被赋予一个数值（权重），可以表示距离、成本、时间或关系强度。

实例

# 一个表示城市间距离的权重图（邻接表形式）
weighted_graph = {
    '北京': {('上海', 1200), ('天津', 100)},  # 北京到上海距离1200，到天津距离100
    '上海': {('北京', 1200), ('杭州', 200)},
    '天津': {('北京', 100)},
    '杭州': {('上海', 200)}
}

关键术语

  • 度 (Degree): 与一个顶点相连的边的数量。在有向图中，分为入度（指向该顶点的边数）和出度（从该顶点指出的边数）。
  • 路径 (Path): 从一个顶点到另一个顶点经过的边序列。如 A -> B -> C。
  • 环/回路 (Cycle): 起点和终点是同一个顶点的路径。
  • 连通图 (Connected Graph): 在无向图中，任意两个顶点间都存在路径。
  • 强连通图 (Strongly Connected Graph): 在有向图中，任意两个顶点间都存在双向路径。

图的存储方式

如何在计算机中表示一个图？主要有两种主流方法。

邻接矩阵

使用一个二维数组（矩阵）matrix 来表示图。matrix[i][j] 的值表示顶点 i 到顶点 j 的边的情况。

  • 对于无向图，矩阵是对称的。
  • 对于权重图，矩阵值存储权重（用特殊值如 0 或 ∞ 表示无边）。
  • 优点：检查任意两个顶点间是否有边非常快（O(1)）。
  • 缺点：占用空间大（O(V^2)），对于边数较少的"稀疏图"浪费空间。

实例

# 使用邻接矩阵表示一个无向图
# 顶点： 0-A, 1-B, 2-C
# 边： A-B, A-C

V = 3  # 顶点数
adj_matrix = [[0] * V for _ in range(V)]

# 添加边 A-B (0-1)
adj_matrix[0][1] = 1
adj_matrix[1][0] = 1  # 无向图需要设置对称位置
# 添加边 A-C (0-2)
adj_matrix[0][2] = 1
adj_matrix[2][0] = 1

print("邻接矩阵：")
for row in adj_matrix:
    print(row)
# 输出：
# [0, 1, 1]
# [1, 0, 0]
# [1, 0, 0]

邻接表

为每个顶点维护一个列表（链表、数组等），记录与其直接相连的所有顶点（及权重）。

  • 优点：空间效率高（O(V + E)），特别适合稀疏图。能快速找到一个顶点的所有邻居。
  • 缺点：检查任意两个顶点间是否有边较慢（O(degree(V))）。

实例

# 使用邻接表（字典+列表）表示同一个无向图
adj_list = {
    'A': ['B', 'C'],  # A 连接着 B 和 C
    'B': ['A'],       # B 连接着 A
    'C': ['A']        # C 连接着 A
}

print("邻接表：")
for vertex, neighbors in adj_list.items():
    print(f"{vertex}: {neighbors}")

图的遍历算法

遍历是图算法的基础，意味着系统地访问图中的每一个顶点。

主要有两种策略：

广度优先搜索

广度优先搜索（BFS）像"水波扩散"一样，从起点开始，先访问所有直接邻居，再访问邻居的邻居，依此类推。它使用队列来实现。

算法步骤：

  1. 将起点放入队列并标记为已访问。
  2. 当队列不为空时： a. 取出队首顶点 v。 b. 访问 v 的所有未访问邻居，将它们放入队列并标记为已访问。
  3. 重复步骤2。

实例

from collections import deque

def bfs(graph, start):
    """使用 BFS 遍历图，返回访问顺序"""
    visited = set([start])  # 记录已访问顶点
    queue = deque([start])  # 初始化队列
    result = []             # 存储访问顺序

    while queue:
        vertex = queue.popleft()
        result.append(vertex)
        # 遍历当前顶点的邻居
        for neighbor in graph[vertex]:
            if neighbor not in visited:
                visited.add(neighbor)
                queue.append(neighbor)
    return result

# 测试数据
test_graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}

print("BFS 遍历顺序（从A开始）:", bfs(test_graph, 'A'))
# 输出可能是: ['A', 'B', 'C', 'D', 'E', 'F']

深度优先搜索

深度优先搜索（DFS）像"走迷宫"一样，选择一条路走到尽头，然后回溯，再走另一条路。它使用栈（或递归）来实现。

递归算法步骤：

  1. 从顶点 v 开始，标记为已访问。
  2. 对于 v 的每一个未访问邻居 u： a. 递归调用 DFS(u)。

实例

def dfs_recursive(graph, vertex, visited=None, result=None):
    """使用递归实现 DFS"""
    if visited is None:
        visited = set()
    if result is None:
        result = []

    visited.add(vertex)
    result.append(vertex)

    for neighbor in graph[vertex]:
        if neighbor not in visited:
            dfs_recursive(graph, neighbor, visited, result)
    return result

print("DFS 遍历顺序（从A开始）:", dfs_recursive(test_graph, 'A'))
# 输出可能是: ['A', 'B', 'D', 'E', 'F', 'C']

图遍历算法对比:

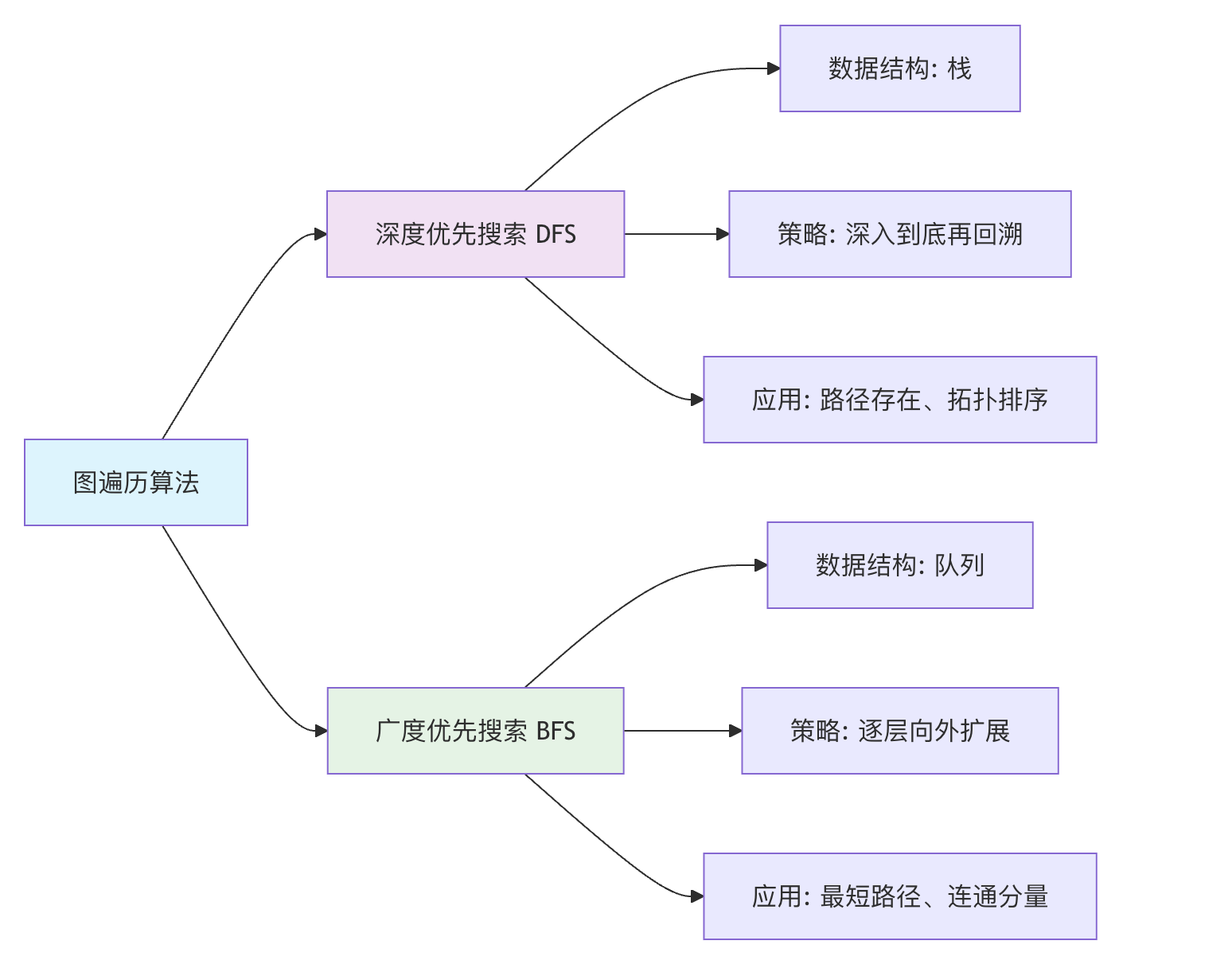
经典应用场景与算法简介

掌握了图的表示和遍历，你就可以探索许多经典问题了：

  1. 最短路径问题：在地图导航中，找到两点间的最短行驶距离。

    • 迪杰斯特拉算法：适用于权重非负的图。
    • 弗洛伊德算法：计算所有顶点对之间的最短路径。

  2. 最小生成树：在保证所有顶点连通的前提下，选择总权重最小的边集（例如，为多个村庄铺设成本最低的光纤网络）。

    • 普里姆算法
    • 克鲁斯卡尔算法

  3. 拓扑排序：对有向无环图（DAG）的顶点进行线性排序，使得对于任何有向边 u->v，u 在排序中都排在 v 之前（例如，安排课程的学习顺序）。