高级树结构
在掌握了二叉树、二叉搜索树等基础树结构后,我们即将踏入一个更广阔、更高效的领域——高级树结构。
如果说基础树是数据结构世界中的普通公路,那么高级树结构就是精心设计的高速公路"和立交桥,它们通过巧妙的平衡规则和存储策略,确保了在数据量巨大或操作频繁时,依然能保持卓越的性能。
本章节将介绍 AVL树、红黑树、B树 和 B+树 这四种经典高级树结构。
为什么需要高级树结构?
在深入学习之前,我们先问一个问题:有了高效的二叉搜索树(BST),为什么还需要更复杂的树?
想象一下,你有一家图书馆,使用 BST 来按书名排序存放书籍。如果你按字母顺序一本一本插入(例如:A..., B..., C...),这棵树会退化成一条链(类似于链表)。这时,查找一本书的时间会从理想的 O(log n) 恶化到最差的 O(n),效率极低。
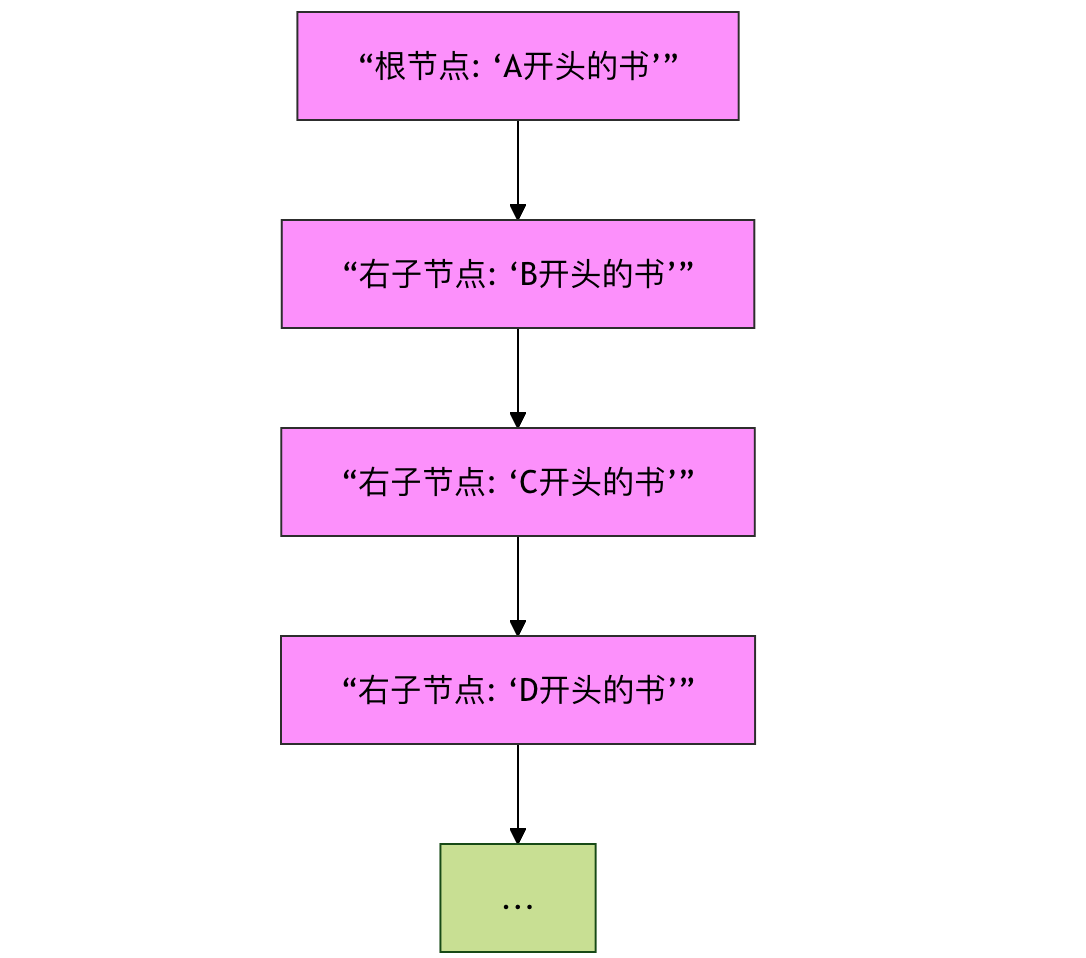
图:二叉搜索树在插入有序数据时退化成链表的示意图,导致查找性能下降。
高级树结构(自平衡树)就是为了解决这个问题而生的。它们会在插入或删除节点时,自动调整树的形态,保持树的平衡,从而确保查找、插入、删除等操作的时间复杂度始终维持在 O(log n) 级别。
AVL 树:高度平衡的守护者
AVL 树是最早被发明的自平衡二叉搜索树,以其发明者 Adelson-Velsky 和 Landis 的名字命名。
AVL 树的核心思想非常简单:对于树中的任意一个节点,其左子树和右子树的高度差不能超过 1。
核心概念:平衡因子
每个节点都有一个 平衡因子,其计算公式为:
平衡因子 = 左子树高度 - 右子树高度
在 AVL 树中,每个节点的平衡因子只能是 -1、0 或 1。
失衡与旋转调整
当插入或删除一个节点后,某个节点的平衡因子变为 2 或 -2,树就失衡了。为了恢复平衡,AVL 树通过四种旋转操作来调整:
- 左旋:处理"右右"失衡情况。
- 右旋:处理"左左"失衡情况。
- 左右旋:先左旋后右旋,处理"左右"失衡情况。
- 右左旋:先右旋后左旋,处理"右左"失衡情况。
实例
def __init__(self, key):
self.key = key
self.height = 1 # 节点高度,初始为1
self.left = None
self.right = None
def get_height(node):
"""获取节点高度(处理空节点)"""
return node.height if node else 0
def get_balance_factor(node):
"""计算节点的平衡因子"""
if not node:
return 0
return get_height(node.left) - get_height(node.right)
def right_rotate(y):
"""
对以y为根的子树进行右旋
y x
/ \ / \
x T4 向右旋转 (y) z y
/ \ - - - - - - - -> / \ / \
z T3 T1 T2 T3 T4
/ \
T1 T2
"""
x = y.left
T3 = x.right
# 执行旋转
x.right = y
y.left = T3
# 更新高度(必须先更新y的高度,再更新x的高度)
y.height = 1 + max(get_height(y.left), get_height(y.right))
x.height = 1 + max(get_height(x.left), get_height(x.right))
# 返回新的根节点
return x
# 左旋函数与右旋对称,此处省略详细实现
def left_rotate(x):
"""对以x为根的子树进行左旋(逻辑与右旋对称)"""
pass
AVL 树的特点总结
| 特点 | 说明 |
|---|---|
| 严格平衡 | 平衡条件严格(高度差≤1),树的高度最接近 log n,查找性能极佳。 |
| 调整频繁 | 插入/删除后可能需要从底向上多次旋转来恢复平衡。 |
| 适用场景 | 适合查询多,增删少的场景,例如数据库索引的中间层或内存中的查找表。 |
红黑树:工程实践的王者
红黑树是另一种自平衡二叉搜索树,它在AVL树的基础上做了一些"妥协"。它不像AVL树那样追求绝对平衡,而是通过一套更宽松的规则来保证大致平衡,从而减少在插入/删除时的旋转次数,在整体性能上取得了更好的工程实践效果。Java的 TreeMap、TreeSet 和 C++ STL 的 map、set 底层都使用了红黑树。
红黑树的五项核心规则
红黑树通过为节点增加颜色属性(红色或黑色)并遵守以下规则来维持平衡:
- 每个节点非红即黑。
- 根节点是黑色的。
- 所有叶子节点(NIL空节点)都是黑色的。
- 红色节点的两个子节点必须是黑色的(即不能有连续的红色节点)。
- 从任一节点到其每个叶子节点的所有路径都包含相同数目的黑色节点。
规则 4 和 5 是红黑树平衡的关键。规则 5 保证了没有一条路径会比其他路径长出两倍以上,从而实现了大致平衡。
插入调整策略
插入新节点时,我们总是先将其着为红色(以避免违反规则 5)。如果这导致了冲突(主要是违反规则 2 或规则 4),则需要通过变色和旋转来调整。调整的核心思路是将冲突(红色)不断向树根方向"上移",直到能够通过变色或旋转解决。
实例
RED = "RED"
BLACK = "BLACK"
def __init__(self, key):
self.key = key
self.color = self.RED # 新节点初始为红色
self.left = None
self.right = None
self.parent = None # 红黑树需要父节点指针
def insert_fixup(tree, node):
"""插入后修复红黑树性质(简化版逻辑描述)"""
while node.parent and node.parent.color == RBNode.RED:
# 情况1:叔叔节点是红色 -> 重新着色
# 情况2 & 3:叔叔节点是黑色 -> 通过旋转和重新着色解决
# ... (具体实现涉及大量指针操作,此处为逻辑描述)
pass
tree.root.color = RBNode.BLACK # 确保根节点为黑
红黑树 vs AVL树
| 特性 | AVL树 | 红黑树 |
|---|---|---|
| 平衡标准 | 严格(高度差≤1) | 宽松(通过颜色规则保证大致平衡) |
| 查找性能 | 更优(树更平衡) | 稍逊,但仍是 O(log n) |
| 插入/删除 | 可能需要更多旋转 | 旋转次数较少,效率更高 |
| 适用场景 | 需要频繁查找的场景 | 综合性能要求高的场景,如语言标准库、文件系统 |
B树与B+树:磁盘存储的引擎
当数据量太大,无法全部装入内存时,就必须存放在磁盘上。磁盘I/O(读写)速度远慢于内存访问。B树和B+树就是为了减少磁盘I/O次数而设计的多路平衡搜索树,它们被广泛用于数据库和文件系统的索引。
B树:平衡多路搜索树
B树不再是一个节点只存一个数据和两个指针。一个 m阶B树 的节点具有以下特性:
- 每个节点最多有 m 个子节点。
- 每个非根、非叶子节点至少有 ⌈m/2⌉ 个子节点。
- 根节点至少有2个子节点(除非它本身是叶子节点)。
- 所有叶子节点都位于同一层。
- 一个非叶子节点如果有 k 个子节点,则它包含 k-1 个键,这些键将子树的值域划分开。
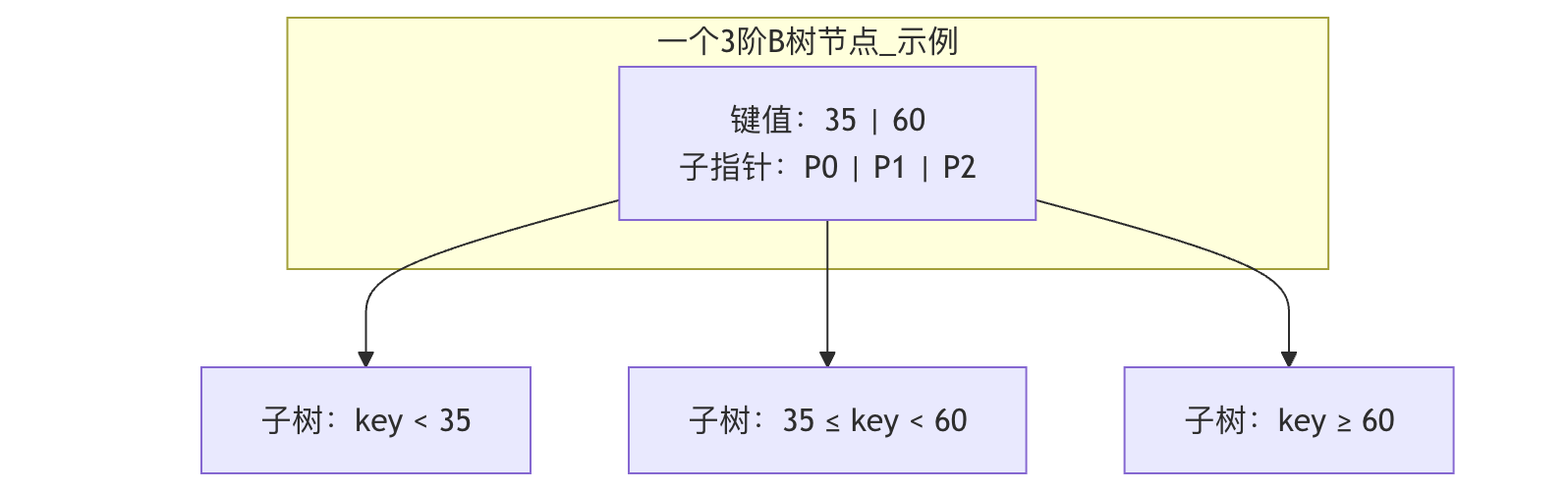
图:一个 3 阶 B 树节点的结构示意图。它包含两个键和三个指针,将数据范围划分为三个区间。
B树的优势在于矮胖的树形。由于一个节点可以存储多个键和拥有多个子节点,树的高度大大降低。查找一个数据时,需要加载的磁盘页面(节点)数就变少了,从而提升了效率。
B+ 树:B 树的升级版
B+ 树在 B 树的基础上做了关键改进,是现代数据库索引的事实标准。
B+树与B树的核心区别:
- 数据存储位置:在 B+ 树中,所有数据记录(或指向记录的指针)只存储在叶子节点中。内部节点(非叶子节点)仅存储键,用于路由。
- 叶子节点链表:所有叶子节点通过指针串联成一个有序双向链表。
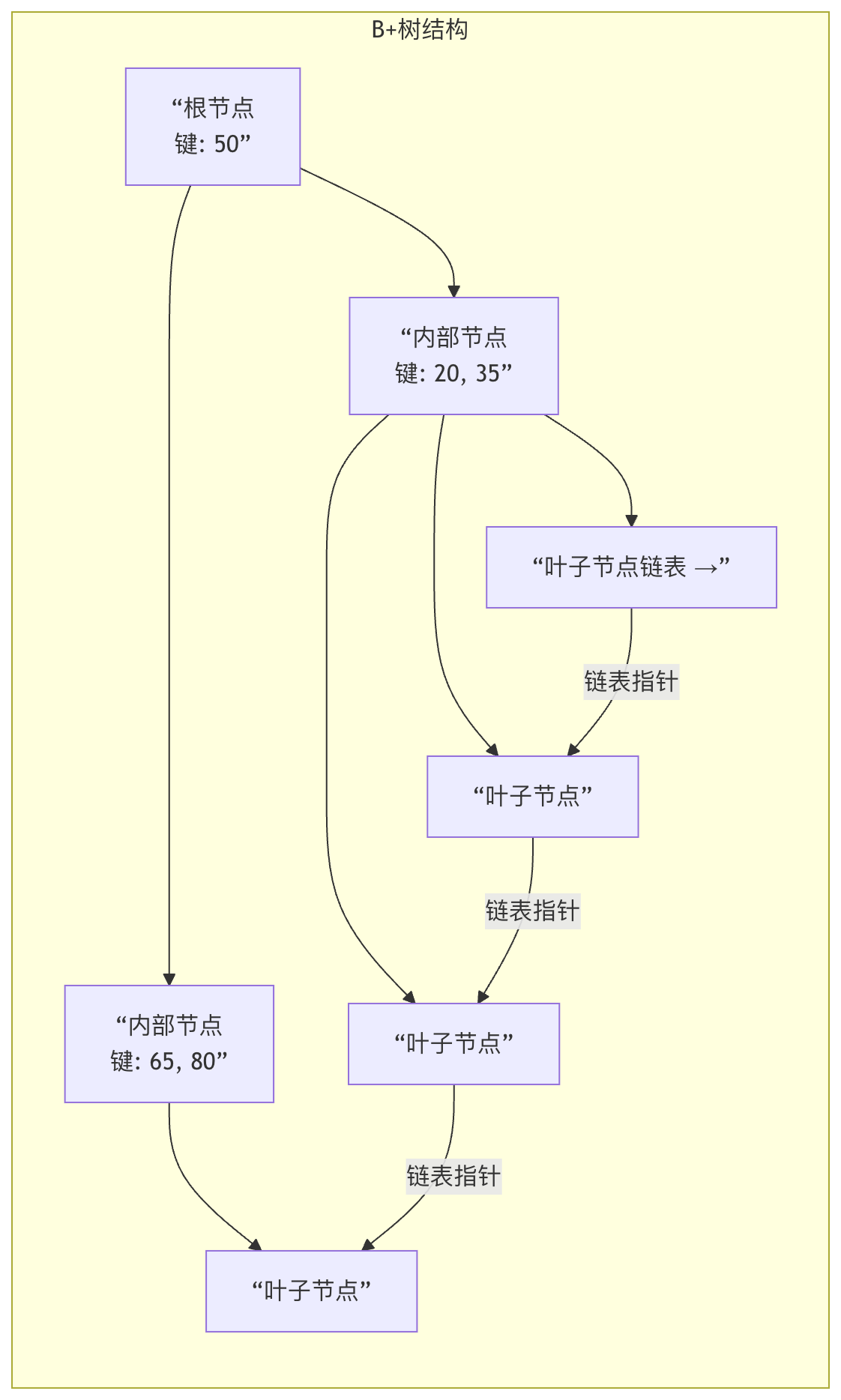
图:B+ 树示意图。注意数据仅在叶子节点,且叶子节点形成有序链表。
B+ 树的巨大优势
| 优势 | 解释 |
|---|---|
| 更稳定的查询效率 | 任何查找都必须走到叶子节点,路径长度相同,性能稳定。 |
| 更高的空间利用率 | 内部节点不存数据,能容纳更多键,树更矮,I/O更少。 |
| 强大的范围查询 | 通过叶子节点的链表,可以高效地进行WHERE age BETWEEN 20 AND 30这类范围查询,而B树需要进行复杂的中序遍历。 |
| 更适合磁盘预读 | 磁盘按页(块)读写。B+树的节点通常设计为恰好一页大小,一次I/O能加载更多键,进一步减少I/O。 |
总结
让我们用一张表格回顾这四种高级树结构:
| 树结构 | 核心目标 | 关键特性 | 典型应用 |
|---|---|---|---|
| AVL 树 | 极致查询速度 | 高度严格平衡,旋转调整频繁 | 内存中需要快速查找的场景 |
| 红黑树 | 综合性能平衡 | 通过颜色规则大致平衡,增删效率高 | 语言标准库(Map/Set)、进程调度 |
| B 树 | 减少磁盘I/O | 多路平衡,数据可存于内部节点 | 早期文件系统、某些数据库索引 |
| B+ 树 | 优化数据库索引 | 数据仅存叶子,叶子成链表,范围查询强 | 现代关系型数据库(MySQL, PostgreSQL)索引 |

点我分享笔记